На рисунке график производной функции

By /

В начале статьи мы рассмотрим важность понимания графического представления производной функции для студентов, изучающих математический анализ. График производной не только помогает визуализировать скорость изменения функции, но и является ключевым инструментом для анализа её свойств, таких как точки экстремума, возрастание и убывание. Этот аспект особенно важен для решения задач оптимизации и понимания поведения функций в различных областях науки и техники.
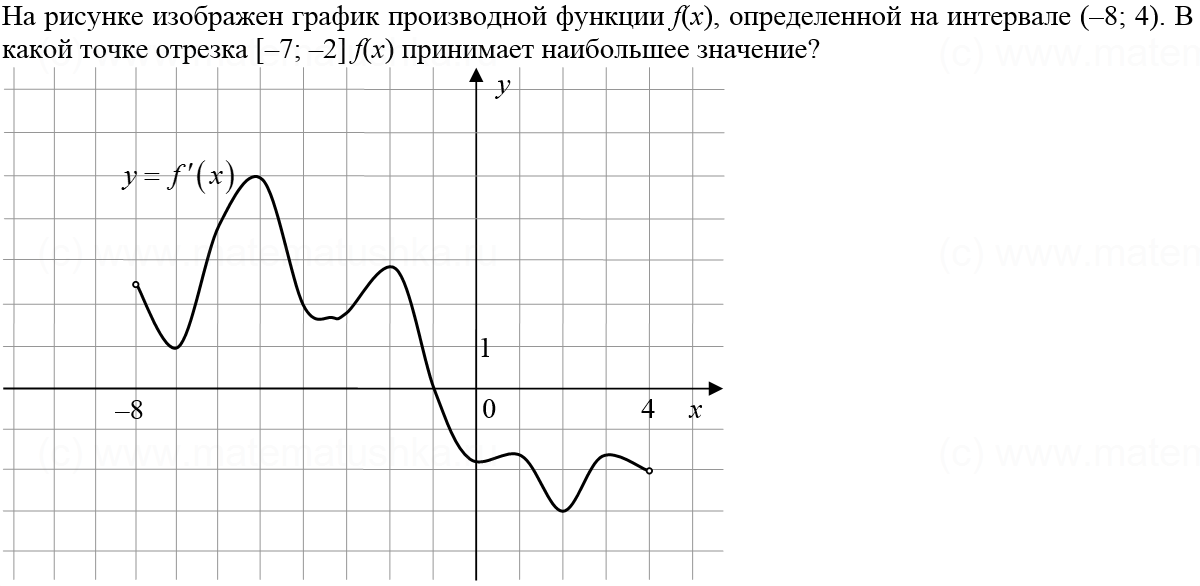
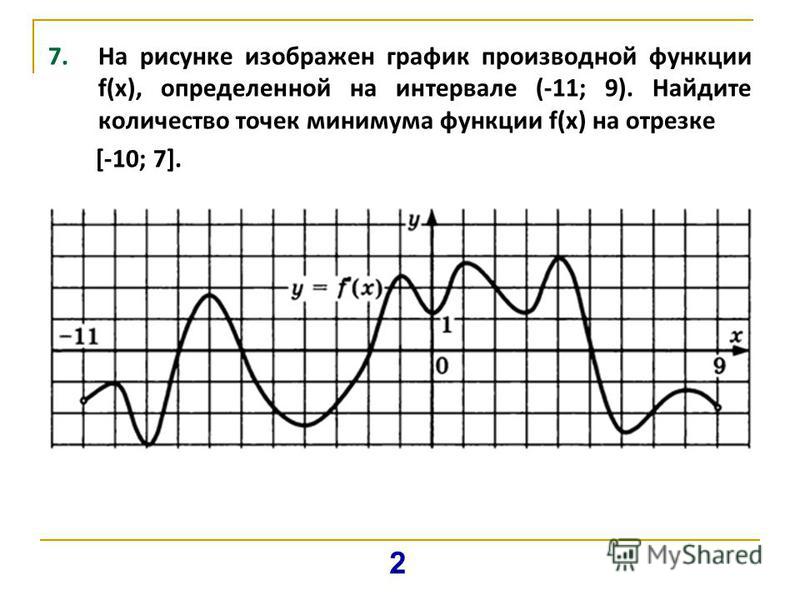
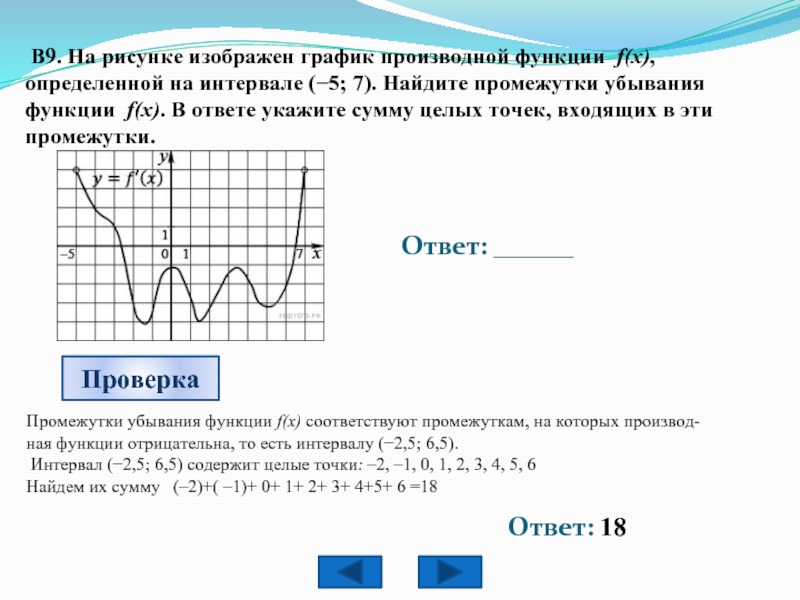
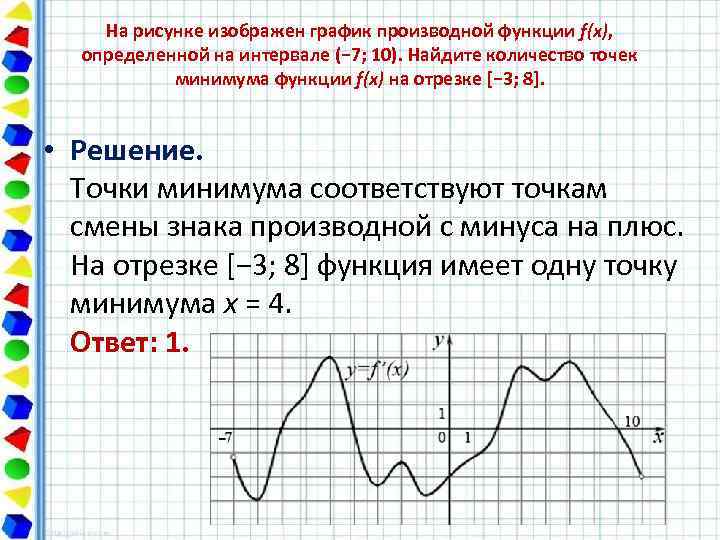
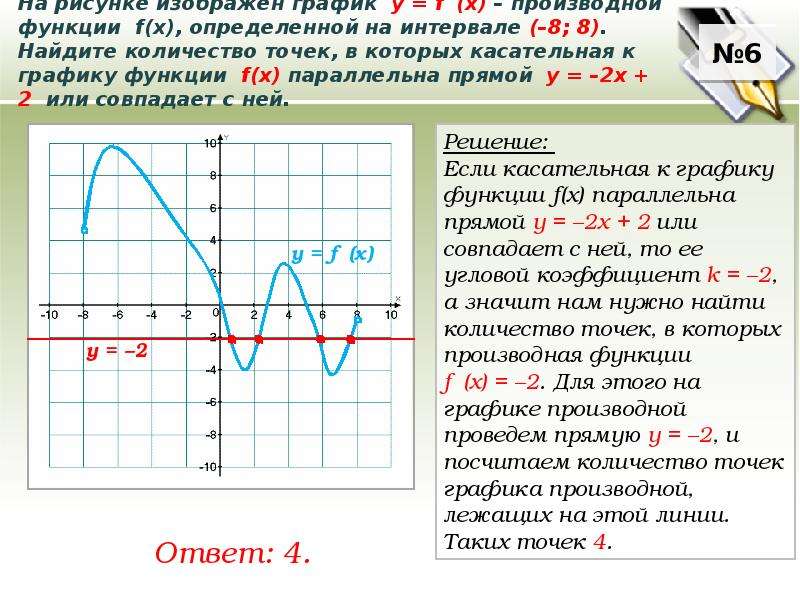
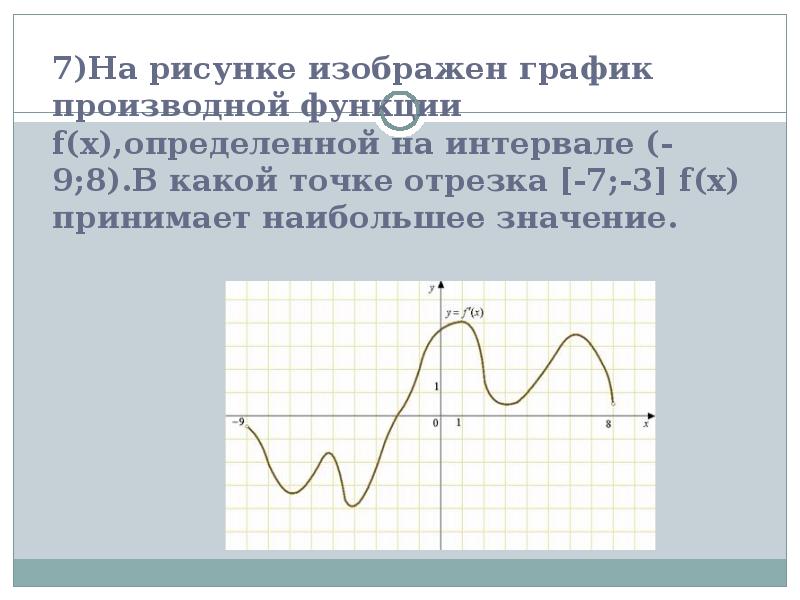
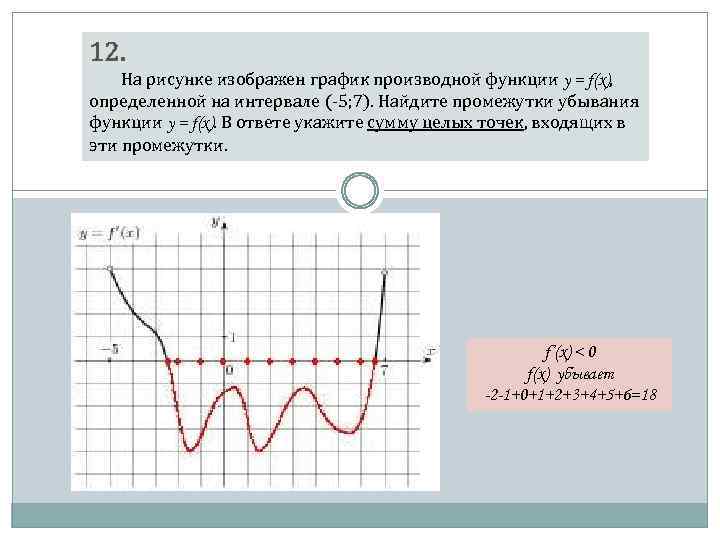
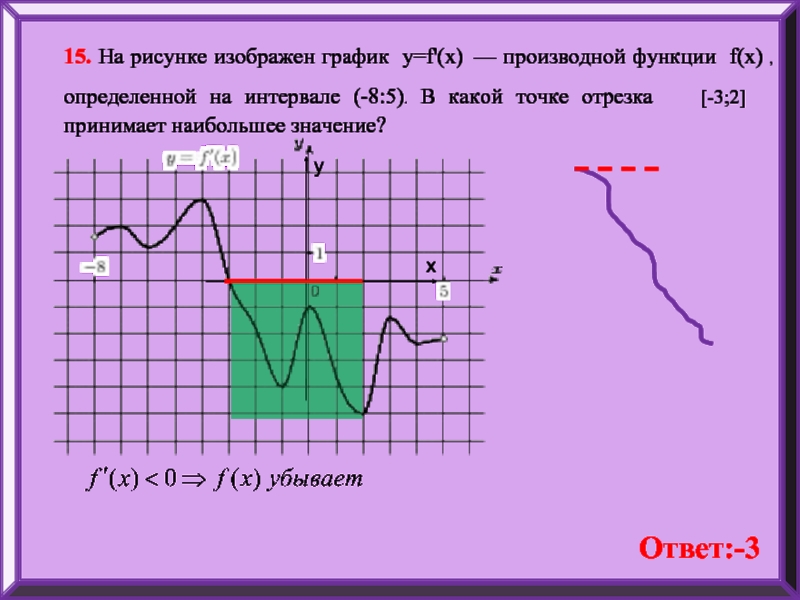
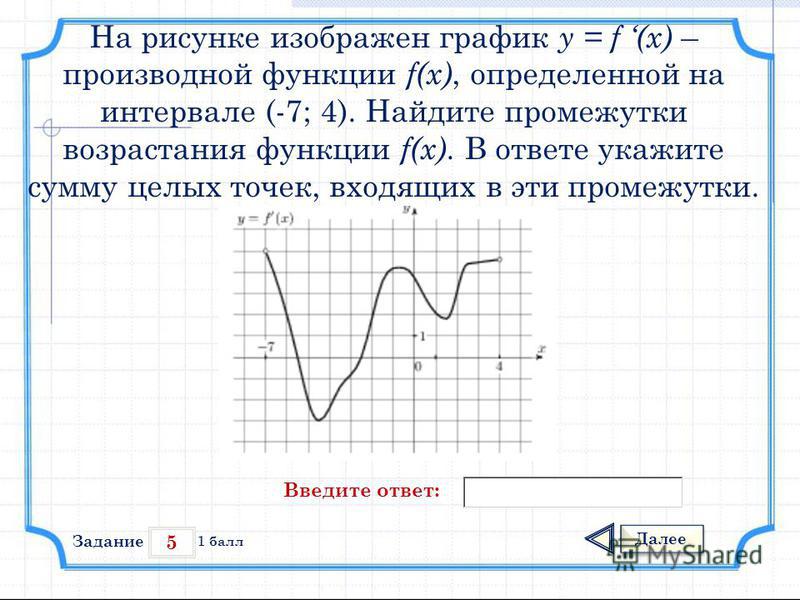
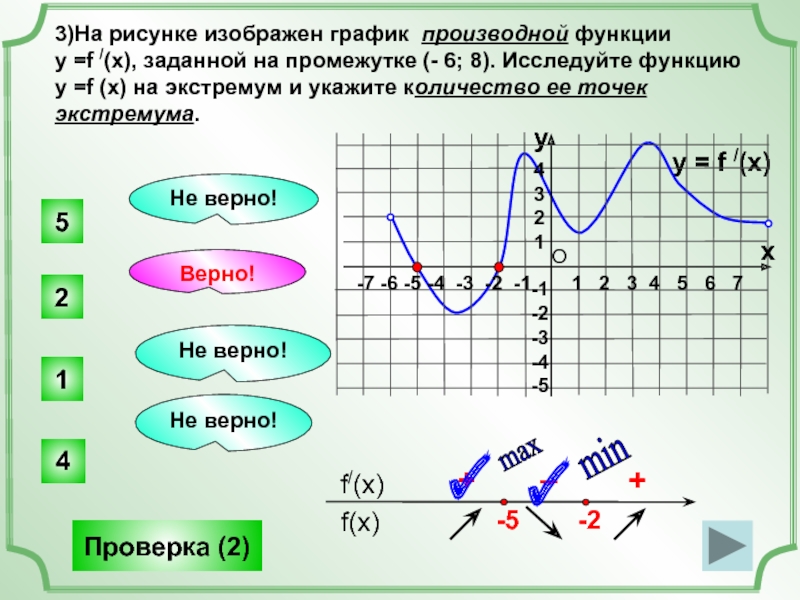
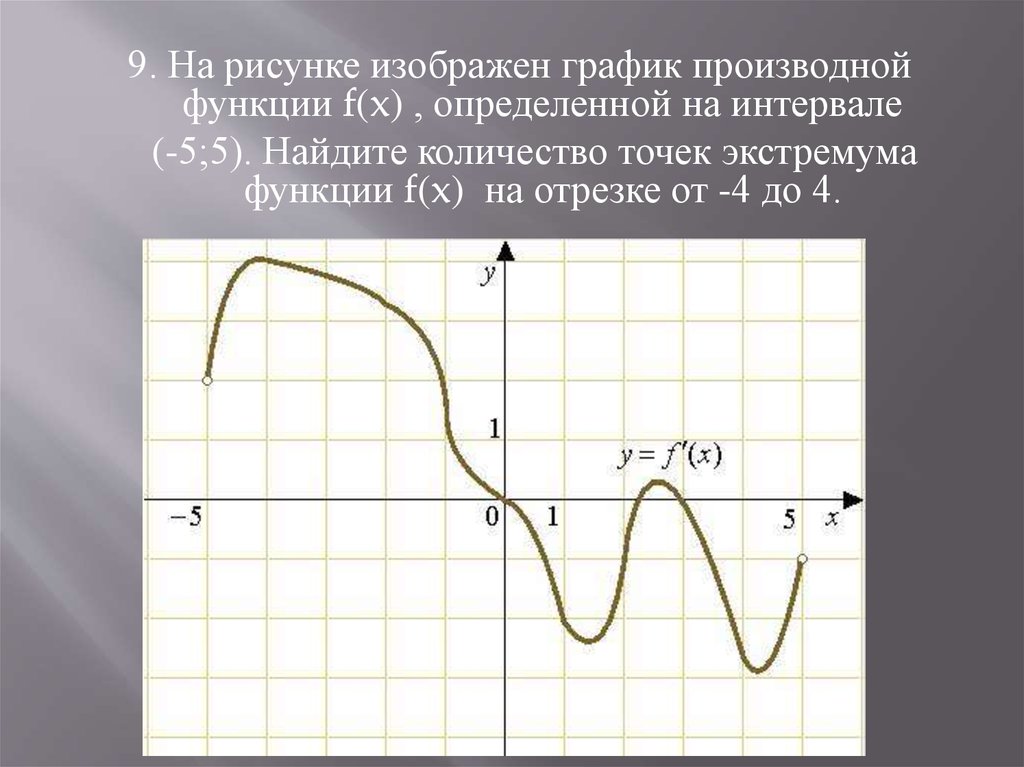
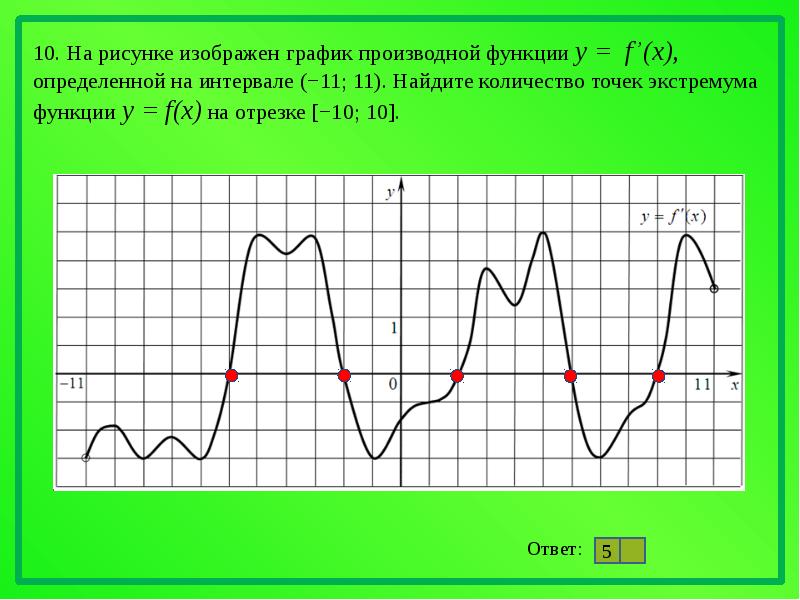
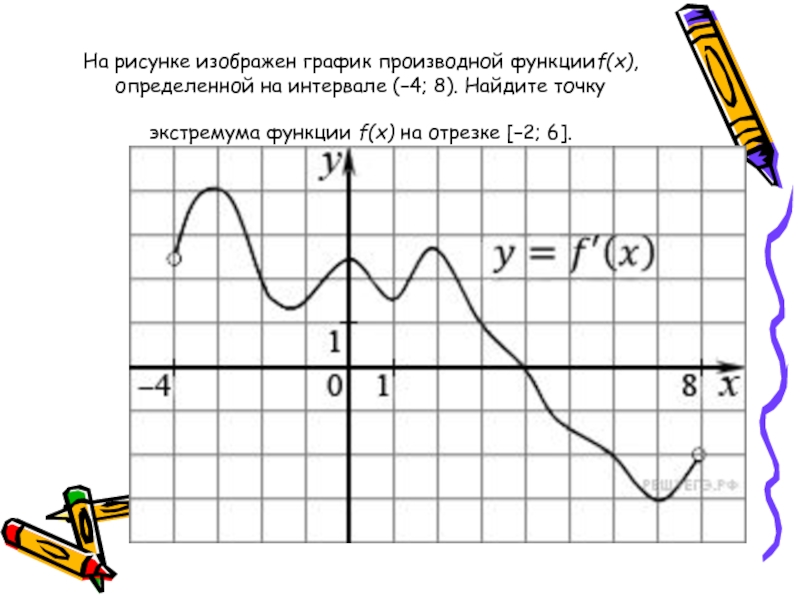
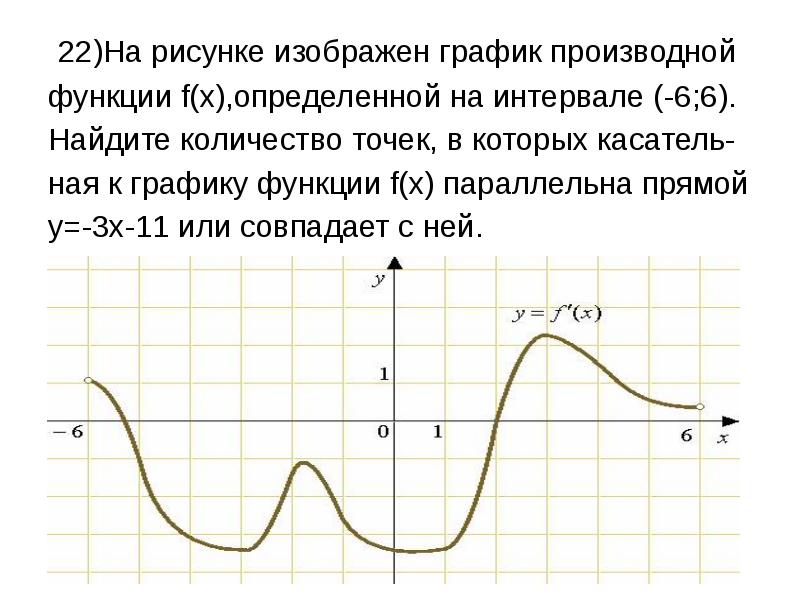
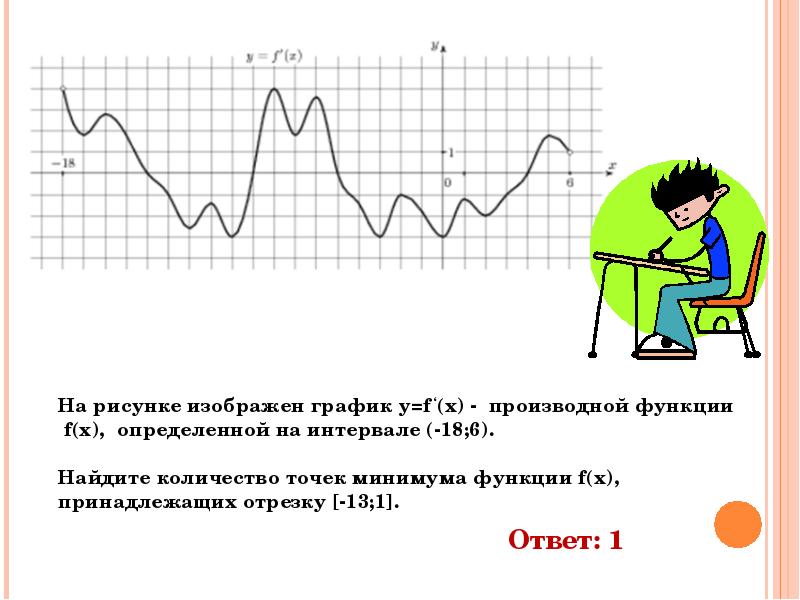
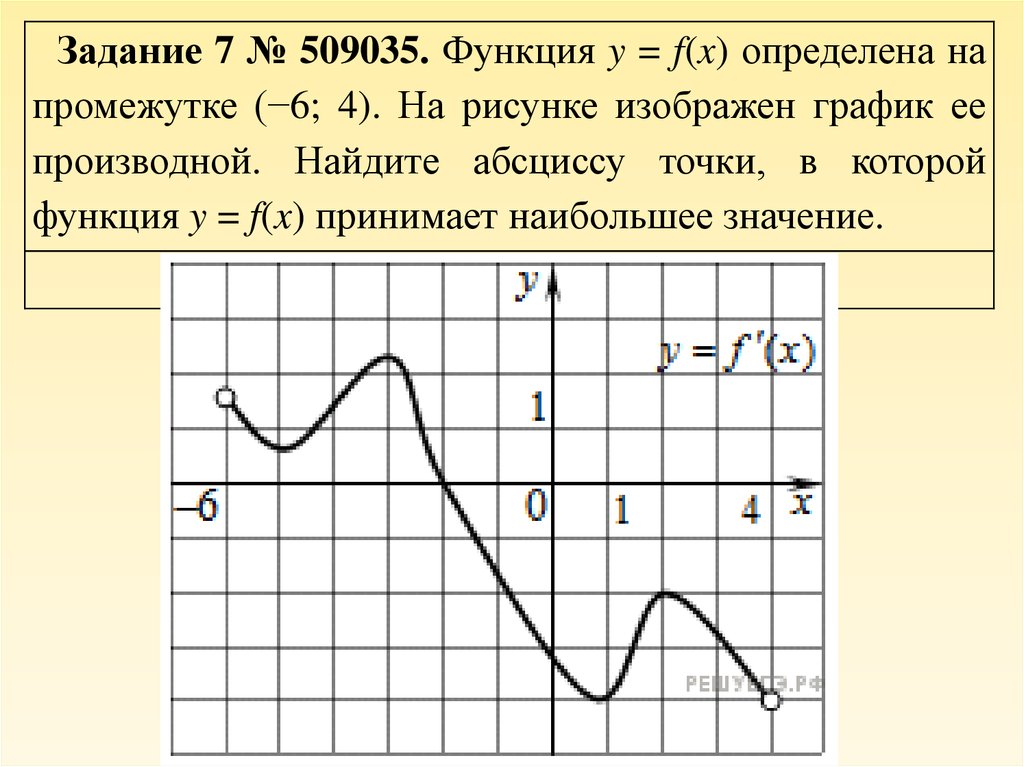
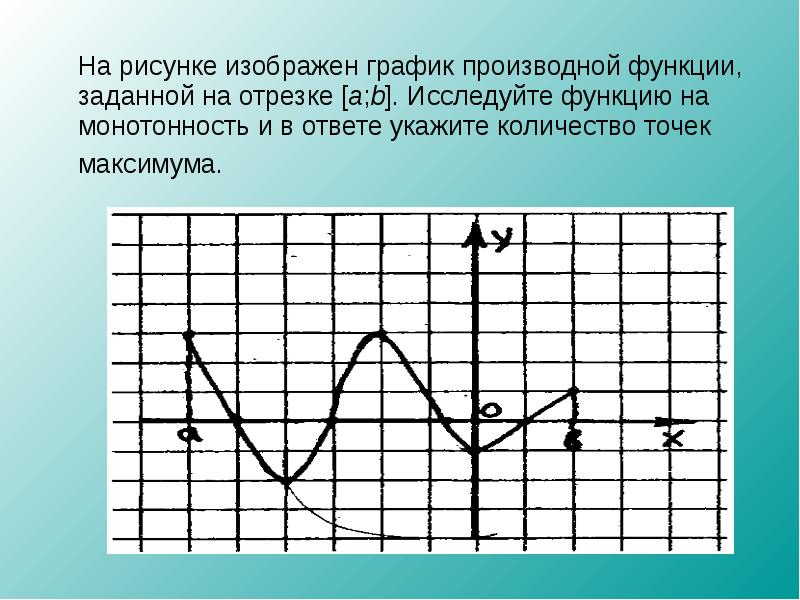
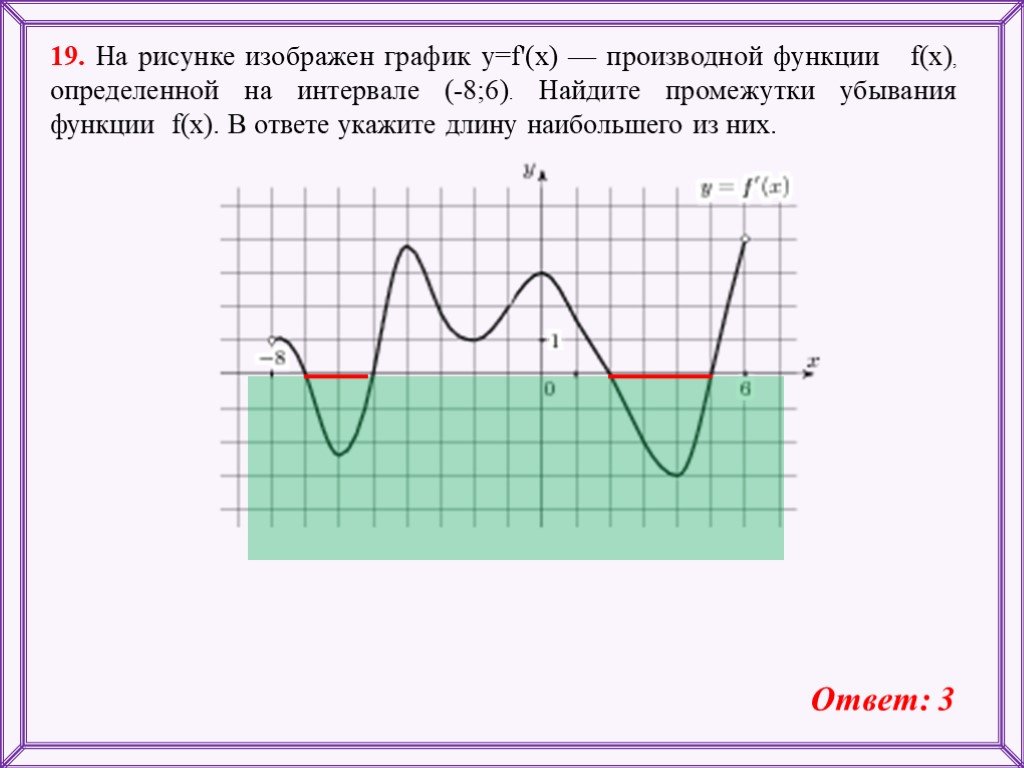
На рисунке график производной функции

На рисунке график производной функции
На рисунке график производной функции. На рисунке изображен график функции. На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. Изобразите график.
На рисунке изображен график функции. На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. Изобразите график.
На рисунке график производной функции. На рисунке изображен график производной. На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. На рисунке изображён график функции производной функции.
На рисунке изображен график производной. На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. На рисунке изображён график функции производной функции.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. График производной функции y=f(x)y=f(x). График y = f '(x) — производной функции f(x). На рисунке изображен график функции y=f(x) определённый на интервале -4 8. На рисунке изображён график производной функции y f x определенной -4 8.
График производной функции y=f(x)y=f(x). График y = f '(x) — производной функции f(x). На рисунке изображен график функции y=f(x) определённый на интервале -4 8. На рисунке изображён график производной функции y f x определенной -4 8.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. Исследование графиков функций. Исследовать график функции. График производной функции. Исследовать функцию по графику.
Исследование графиков функций. Исследовать график функции. График производной функции. Исследовать функцию по графику.
На рисунке график производной функции
На рисунке график производной функции. График производной второго порядка. Производной в экономике графики. Анализ производной по графику функции. На рисунке изображен график производной . Тогда:.
График производной второго порядка. Производной в экономике графики. Анализ производной по графику функции. На рисунке изображен график производной . Тогда:.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. Касательная параллельна прямой или совпадает с ней. Касательная к графику производной параллельна прямой. Функция f x определена и дифференцируема на интервале -2 10. График производной х3.
Касательная параллельна прямой или совпадает с ней. Касательная к графику производной параллельна прямой. Функция f x определена и дифференцируема на интервале -2 10. График производной х3.
На рисунке график производной функции. На рисунке изображён график производной функции f x - 5 5. На рисунке изображен график производной функции f x на интервале -8 8. На рисунке изображен график производной функции y f x. На рисунке изображен график производной функции f x.
На рисунке изображён график производной функции f x – 5 5. На рисунке изображен график производной функции f x на интервале -8 8. На рисунке изображен график производной функции y f x. На рисунке изображен график производной функции f x.
На рисунке график производной функции. Производная касательная к графику. Касательная к графику производной. Производная и касательная к графику функции. График производной функции и график функции.
Производная касательная к графику. Касательная к графику производной. Производная и касательная к графику функции. График производной функции и график функции.
На рисунке график производной функции. На рисунке изображен график производной функции f x. На рисунке изображён график производной Найдите промежутки убывания. На рисунке изображен график производной функции. На рисунке график производной функции определенной на интервале.
На рисунке изображен график производной функции f x. На рисунке изображён график производной Найдите промежутки убывания. На рисунке изображен график производной функции. На рисунке график производной функции определенной на интервале.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. Найдите промежутки возрастания функции график производной функции. Возрастание функции на графике производной. График производной промежутки возрастания. Промежутки возрастания функции на графике.
Найдите промежутки возрастания функции график производной функции. Возрастание функции на графике производной. График производной промежутки возрастания. Промежутки возрастания функции на графике.
На рисунке график производной функции. График функции производной и первообразной. Производная функции. Производная функции ЕГЭ. График производной функции.
График функции производной и первообразной. Производная функции. Производная функции ЕГЭ. График производной функции.
На рисунке график производной функции. Максимум функции на графике производной. Точки максимума Графика производной функции. График производной функции минимум и максимум. Точка максимума функции производной ЕГЭ.
Максимум функции на графике производной. Точки максимума Графика производной функции. График производной функции минимум и максимум. Точка максимума функции производной ЕГЭ.
На рисунке график производной функции. На рисунке изображен график функции y f x (8 3). На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. Нарисовать график производной.
На рисунке изображен график функции y f x (8 3). На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. Нарисовать график производной.
На рисунке график производной функции
На рисунке график производной функции. Найдите количество точек экстремума функции f(x). Кол во точек экстремума функции. Найдите количество точек экстремума функции. Количество точек экстремума функции на графике.
Найдите количество точек экстремума функции f(x). Кол во точек экстремума функции. Найдите количество точек экстремума функции. Количество точек экстремума функции на графике.
На рисунке график производной функции. На рисунке изображен график функции y f 'x производной функции -5 5. На рисунке изображен график функции y f x определенной на интервале. На рисунке изображен график функции y f x определите на интервале -5 5. На рисунке изображён график функции y f x определённой на интервале -8 5.
На рисунке изображен график функции y f ‘x производной функции -5 5. На рисунке изображен график функции y f x определенной на интервале. На рисунке изображен график функции y f x определите на интервале -5 5. На рисунке изображён график функции y f x определённой на интервале -8 5.
На рисунке график производной функции. График производной f(x). Y F X график производной. График производной функции y=f(x)y=f(x). Производная y=f(x) график.
График производной f(x). Y F X график производной. График производной функции y=f(x)y=f(x). Производная y=f(x) график.
На рисунке график производной функции. Найдите абсциссу точки в которой касательная к графику функции. График производной y=2x-2. На рисунке изображен график производной функции. На рисунке изображён график функции производной функции.
Найдите абсциссу точки в которой касательная к графику функции. График производной y=2x-2. На рисунке изображен график производной функции. На рисунке изображён график функции производной функции.
На рисунке график производной функции. Изображен график производной функции. Количество точек минимума. Количество точек минимума функции. Найдите Кол-во точек минимума функции.
Изображен график производной функции. Количество точек минимума. Количество точек минимума функции. Найдите Кол-во точек минимума функции.
На рисунке график производной функции. Как по графику производной найти количество точек экстремума. На рисунке изобрахён график ф. На рисунке изображен график производной. На рисунке изображен график производной функции.
Как по графику производной найти количество точек экстремума. На рисунке изобрахён график ф. На рисунке изображен график производной. На рисунке изображен график производной функции.
На рисунке график производной функции. На рисунке изображен график производной функции. В какой точке производная принимает наибольшее значение. Функция принимает наибольшее значение. График функции на отрезке.
На рисунке изображен график производной функции. В какой точке производная принимает наибольшее значение. Функция принимает наибольшее значение. График функции на отрезке.
На рисунке график производной функции. Промежутки возрастания функции на графике производной. На рисунке изображен график производной. Промежутки возрастания функции на графике. Сумму целых точек, входящих в эти промежутки..
Промежутки возрастания функции на графике производной. На рисунке изображен график производной. Промежутки возрастания функции на графике. Сумму целых точек, входящих в эти промежутки..
На рисунке график производной функции
На рисунке график производной функции. Как найти наименьшее значение функции по графику производной. Когда функция принимает наименьшее значение на графике производной. Как определить наименьшее значение функции по графику производной. Где наименьшее значение производной на графике функции.
Как найти наименьшее значение функции по графику производной. Когда функция принимает наименьшее значение на графике производной. Как определить наименьшее значение функции по графику производной. Где наименьшее значение производной на графике функции.
На рисунке график производной функции. На рисунке изображен график производной функции f x. На графике изображен график функции y f x производной функции. На рисунке изображен график производной функции y f x. На рисунке изображён график функции y f x производной функции.
На рисунке изображен график производной функции f x. На графике изображен график функции y f x производной функции. На рисунке изображен график производной функции y f x. На рисунке изображён график функции y f x производной функции.
На рисунке график производной функции. На рисунке изображен график производной функции f x на интервале -8 3. График производной функции f x. На рисунке изображён график функции производной функции. На рисунке изображён график функции f x.
На рисунке изображен график производной функции f x на интервале -8 3. График производной функции f x. На рисунке изображён график функции производной функции. На рисунке изображён график функции f x.
На рисунке график производной функции. График функции y f x производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции. Функция принимает наименьшее значение.
График функции y f x производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции. Функция принимает наименьшее значение.
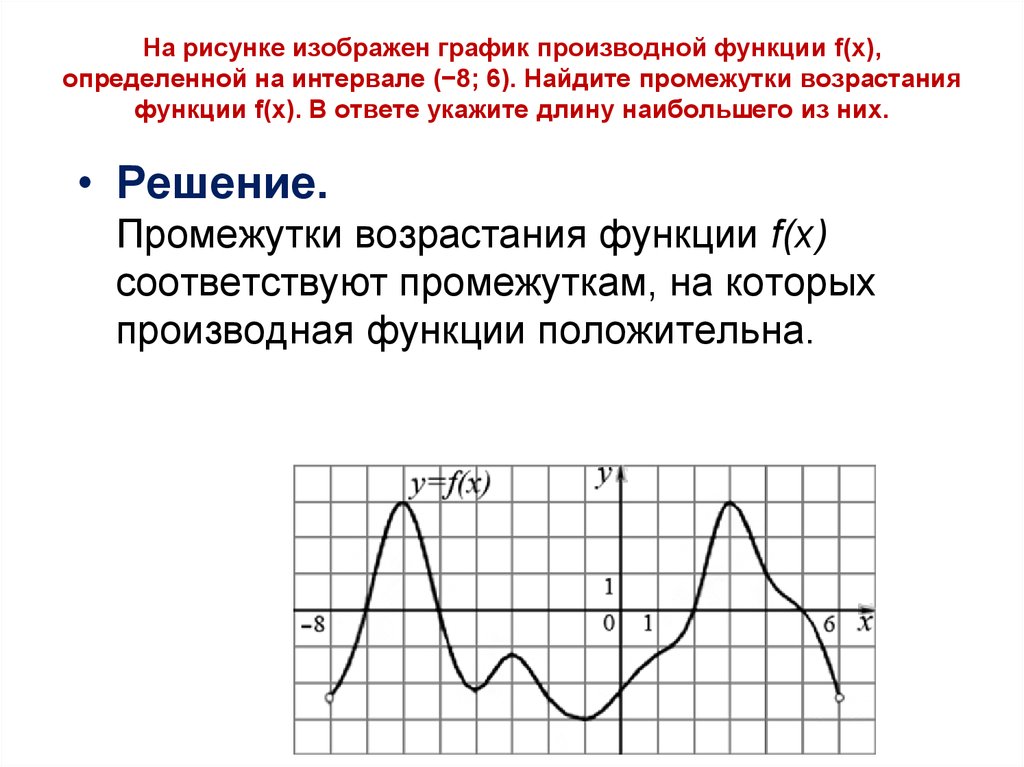
На рисунке график производной функции
На рисунке график производной функции. График производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции f x. Найдите количество точек максимума функции f x.
График производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции f x. Найдите количество точек максимума функции f x.
На рисунке график производной функции. Точки минимума функции f x. Найдите количество точек максимума функции f x. График производной найти точки минимума функции. Найдите количество точек минимума функции.
Точки минимума функции f x. Найдите количество точек максимума функции f x. График производной найти точки минимума функции. Найдите количество точек минимума функции.
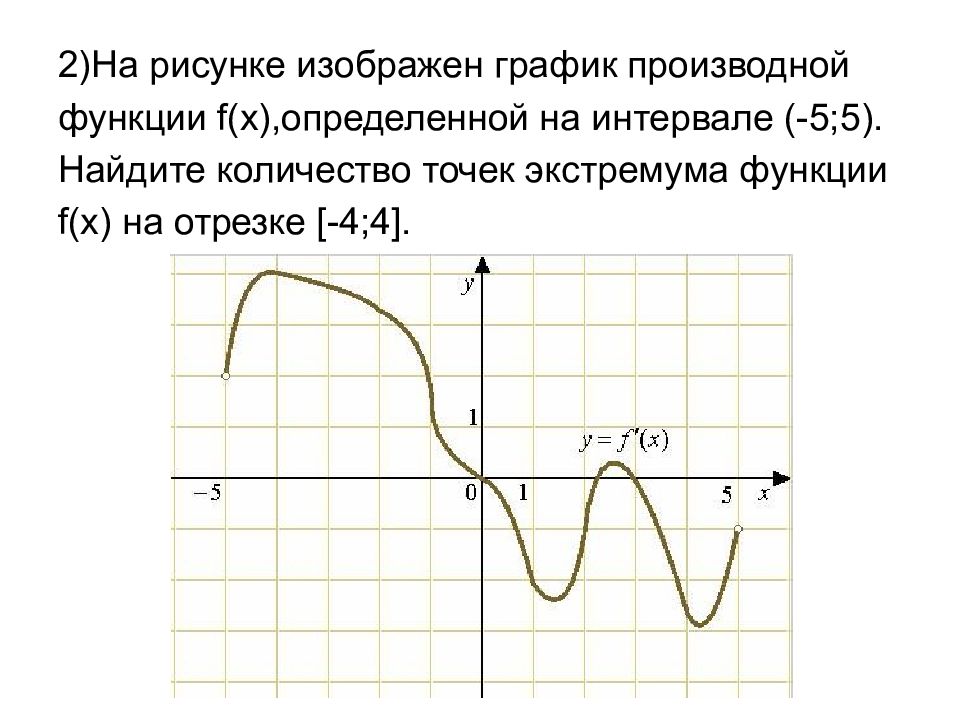
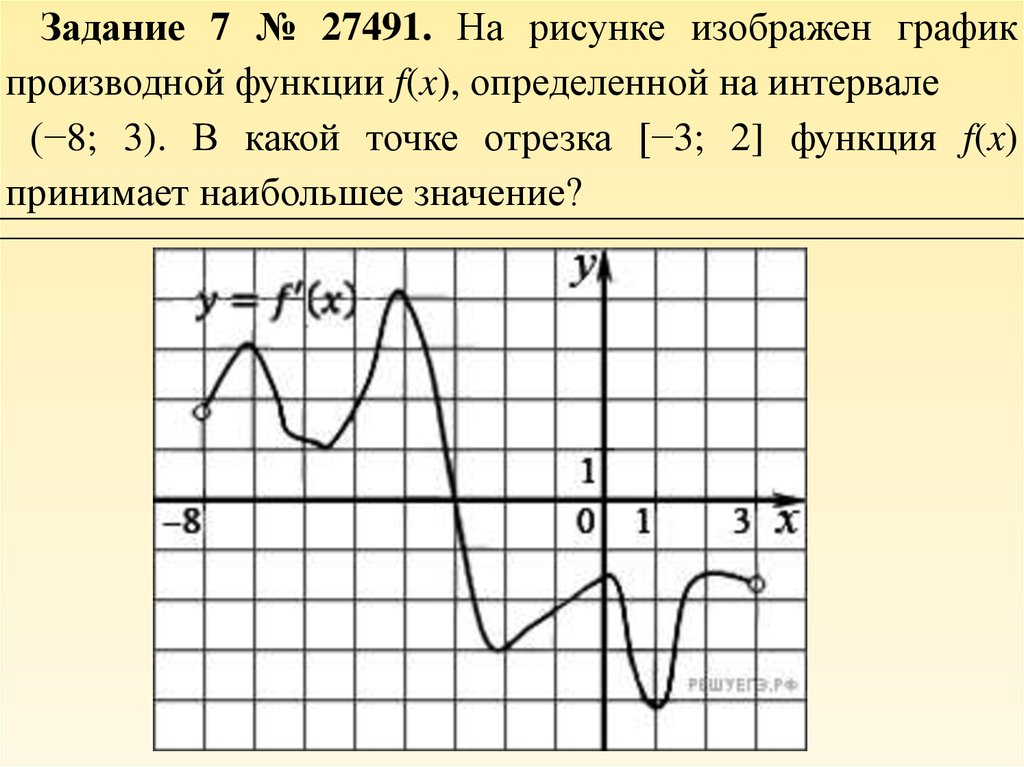
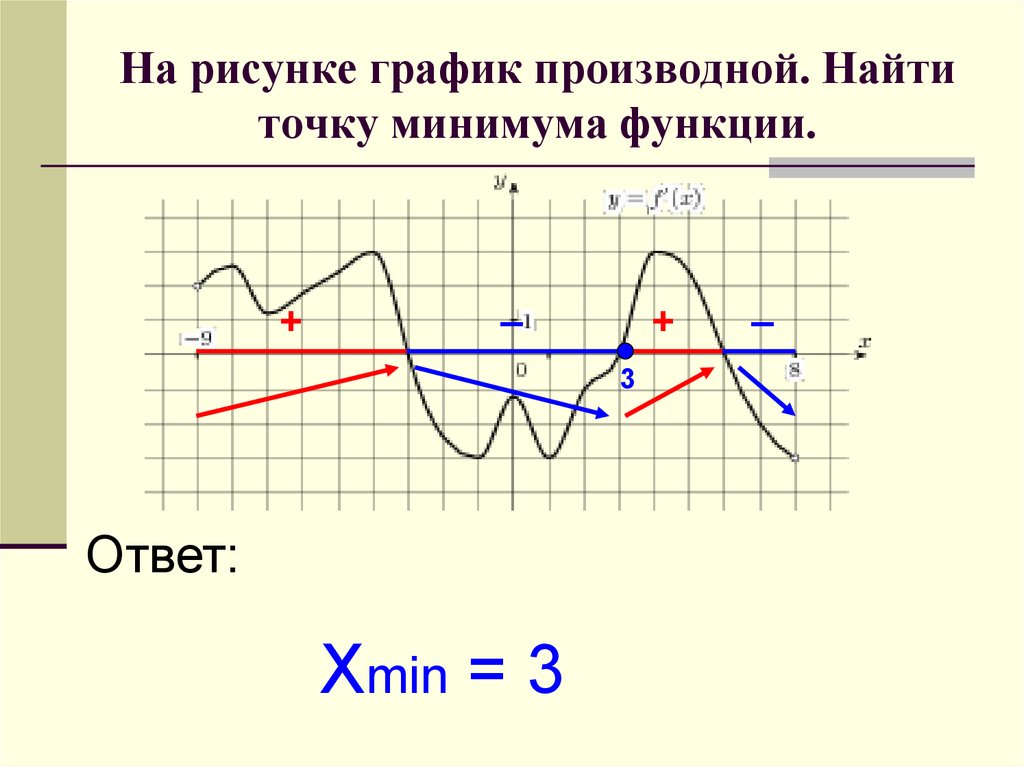
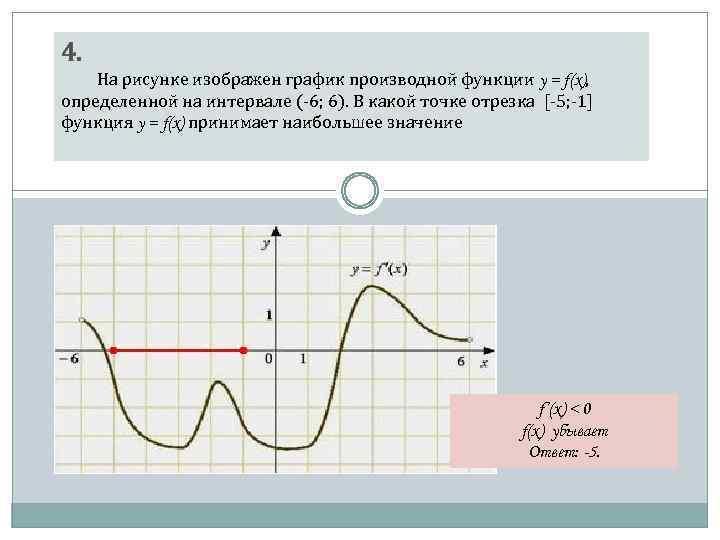
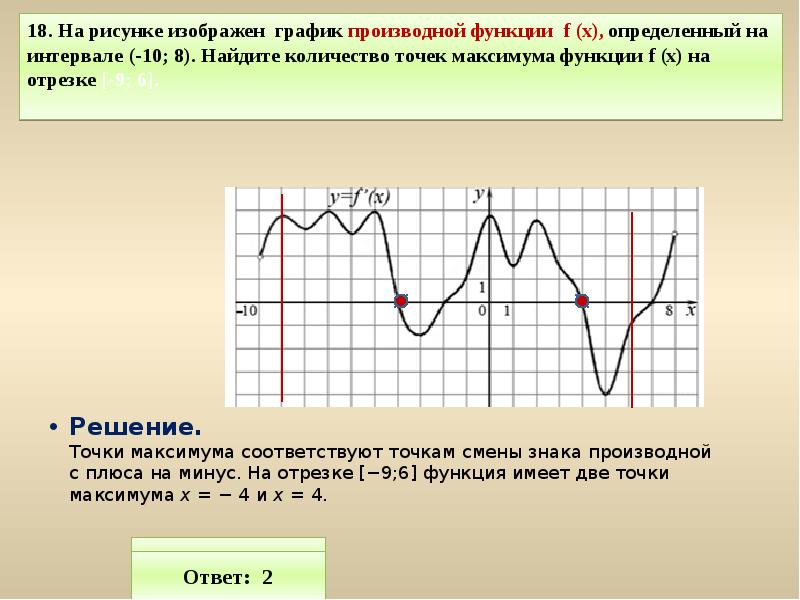
На рисунке график производной функции
На рисунке график производной функции. Точки максимума функции на графике производной функции. Точки максимума функции на графике производной. Точки максимума на графике производной. Точка максимума производной функции.
Точки максимума функции на графике производной функции. Точки максимума функции на графике производной. Точки максимума на графике производной. Точка максимума производной функции.
На рисунке график производной функции. На рисунке изображен график. На рисунке график производной функции определенной на интервале. Касательная к графику производной параллельна. На рисунке изображен график касательная к графику параллельна прямой.
На рисунке изображен график. На рисунке график производной функции определенной на интервале. Касательная к графику производной параллельна. На рисунке изображен график касательная к графику параллельна прямой.
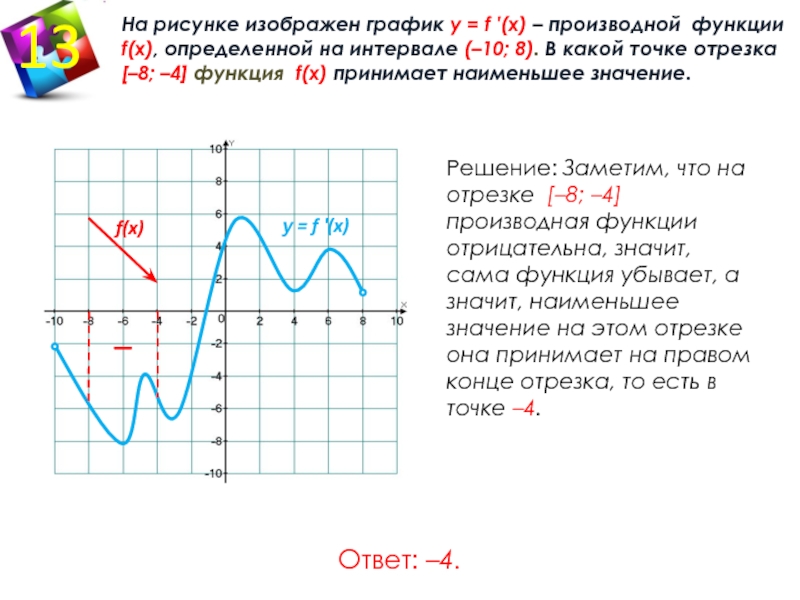
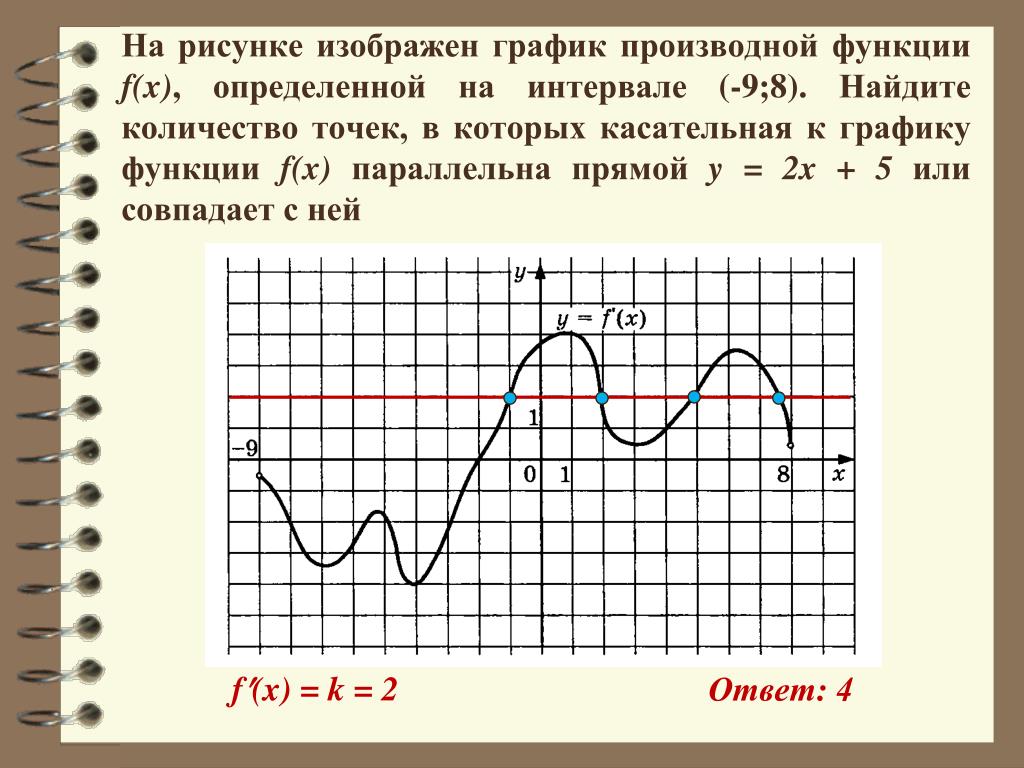
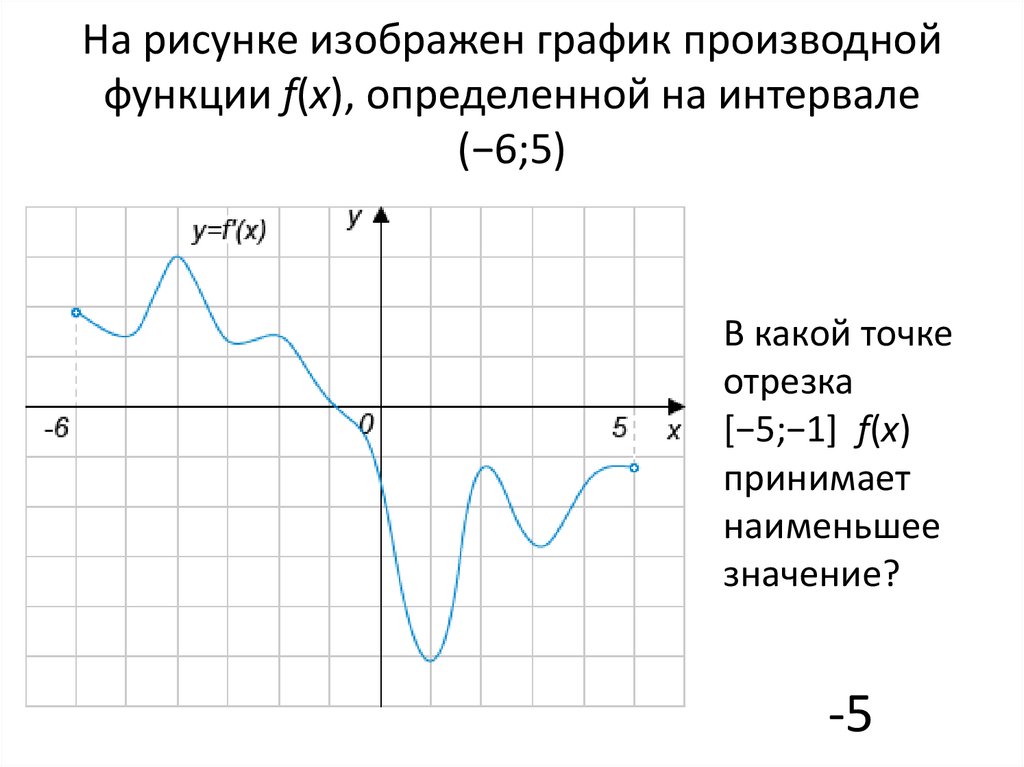
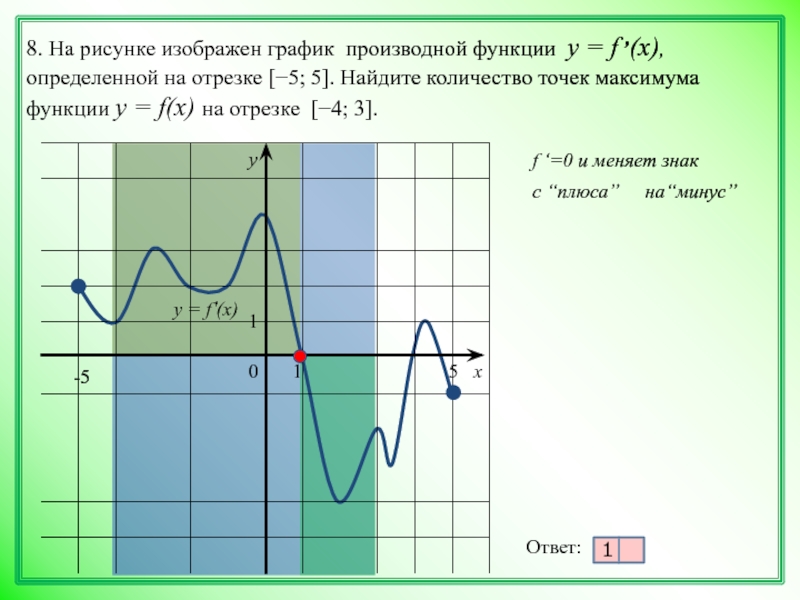
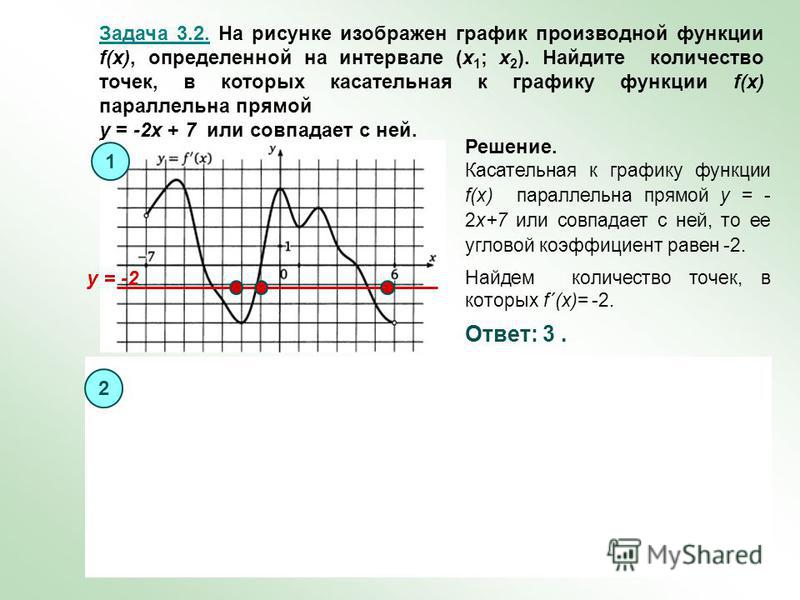
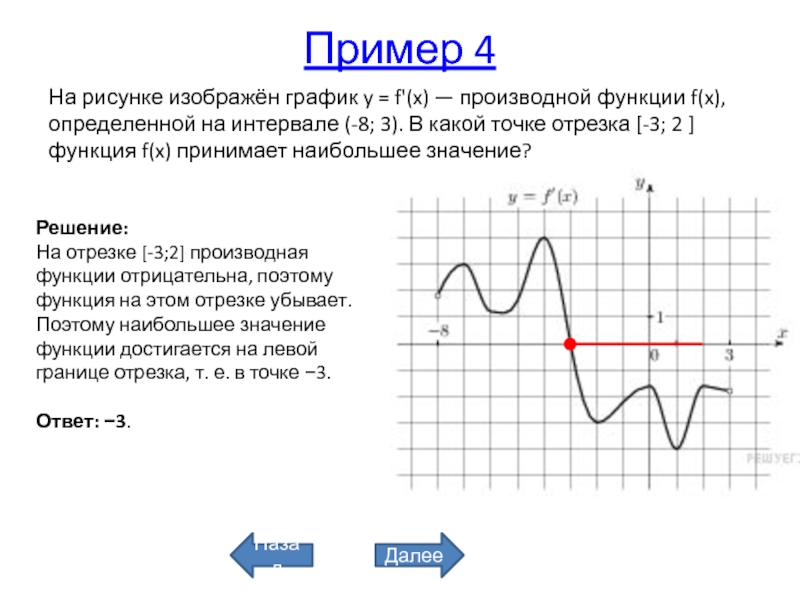
На рисунке график производной функции
На рисунке график производной функции. Изображен график производной функции. На рисунке изображен график производной функции. Изображение производной на графике. На рисунке изображен график производной функции f x.
Изображен график производной функции. На рисунке изображен график производной функции. Изображение производной на графике. На рисунке изображен график производной функции f x.
На рисунке график производной функции. Промежутки убывания функции на графике производной. Промежутки убывания на графике производной. На рисунке изображен график производной. На рисунке изображен график производной функции.
Промежутки убывания функции на графике производной. Промежутки убывания на графике производной. На рисунке изображен график производной. На рисунке изображен график производной функции.
На рисунке график производной функции. Функция определена на интервале. График производной функции. На рисунке изображен график. На рисунке изображен график производной.
Функция определена на интервале. График производной функции. На рисунке изображен график. На рисунке изображен график производной.
На рисунке график производной функции. График производной f (x)=0. График функции y f x производной функции f x. График производной возрастает если. Как находится производная по графику.
График производной f (x)=0. График функции y f x производной функции f x. График производной возрастает если. Как находится производная по графику.
На рисунке график производной функции. На рисунке изображен график производной. На рисунке изображен график производной функции f x. Промежутки возрастания функции на графике производной функции. На рисунке изображен график производной функции.
На рисунке изображен график производной. На рисунке изображен график производной функции f x. Промежутки возрастания функции на графике производной функции. На рисунке изображен график производной функции.
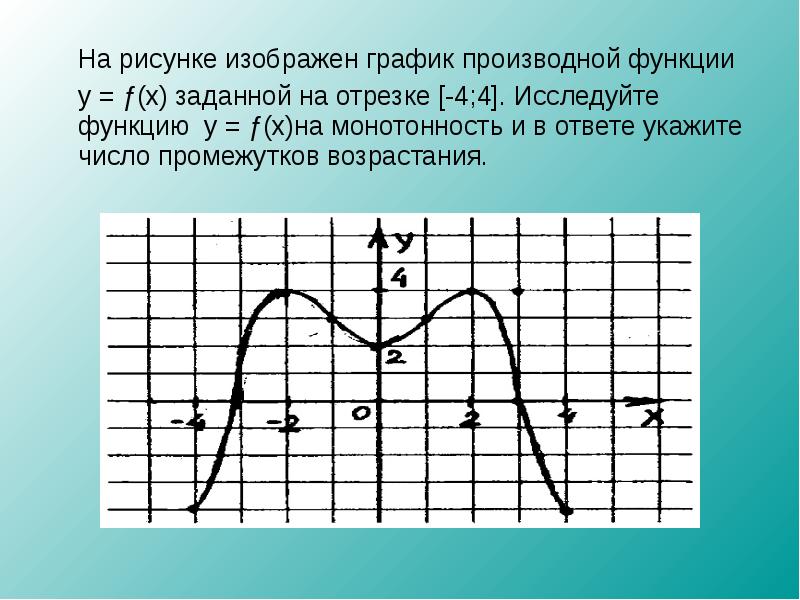
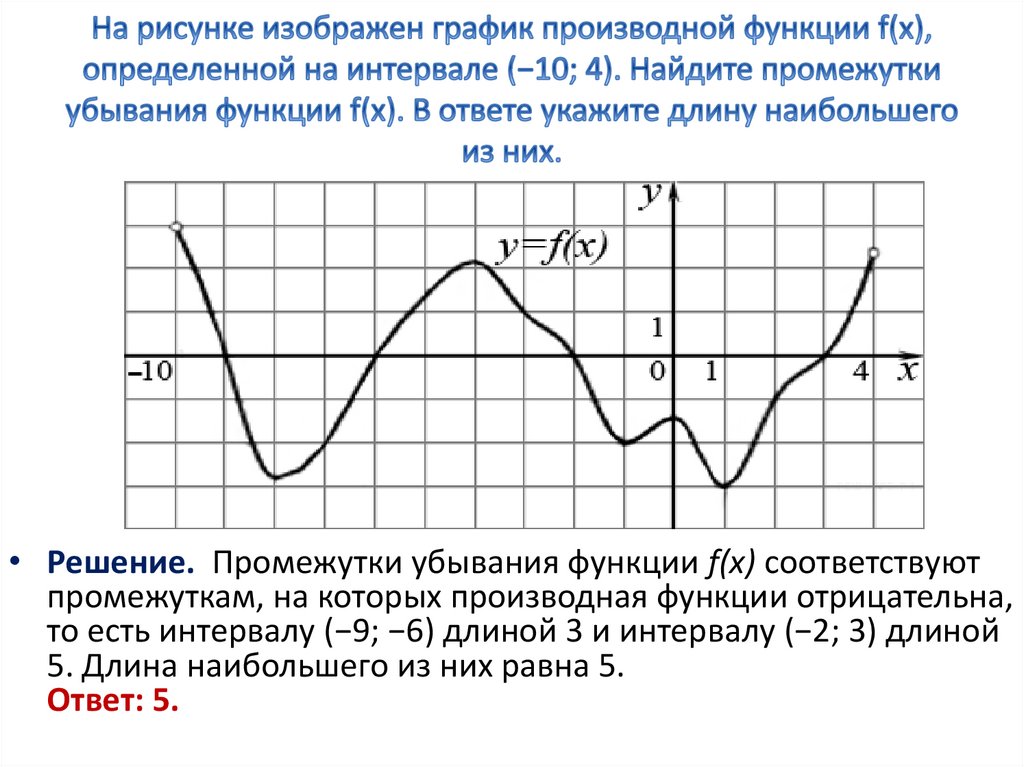
На рисунке график производной функции
На рисунке график производной функции. Найдите промежутки возрастания функции график производной функции. Возрастание на графике производной функции f. График производной где функция убывает. Промежутки возрастания функции f x.
Найдите промежутки возрастания функции график производной функции. Возрастание на графике производной функции f. График производной где функция убывает. Промежутки возрастания функции f x.
На рисунке график производной функции. Производная по графику функции. Нахождение производной по графику. Производная Графика фунцкций. Производная на графике.
Производная по графику функции. Нахождение производной по графику. Производная Графика фунцкций. Производная на графике.
На рисунке график производной функции. График y = f '(x) — производной функции f(x). На рисунке изображен график y=f x производной. На рисунке график производной функции определенной на интервале. На рисунке изображён график y f x производной функции f x.
График y = f '(x) — производной функции f(x). На рисунке изображен график y=f x производной. На рисунке график производной функции определенной на интервале. На рисунке изображён график y f x производной функции f x.
На рисунке график производной функции. Функция f x определена на промежутке [-6 6] на рисунке изображен график.. Найдите промежутки возрастания функции график производной функции. График функции f(x), определенной на интервале (-6; 6).. Промежутки возрастания функции в ответ укажите сумму целых точек.
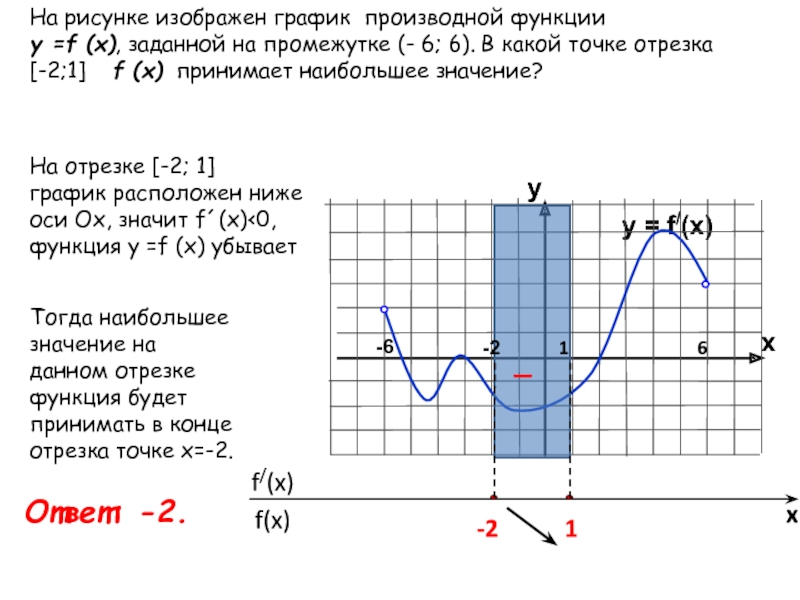
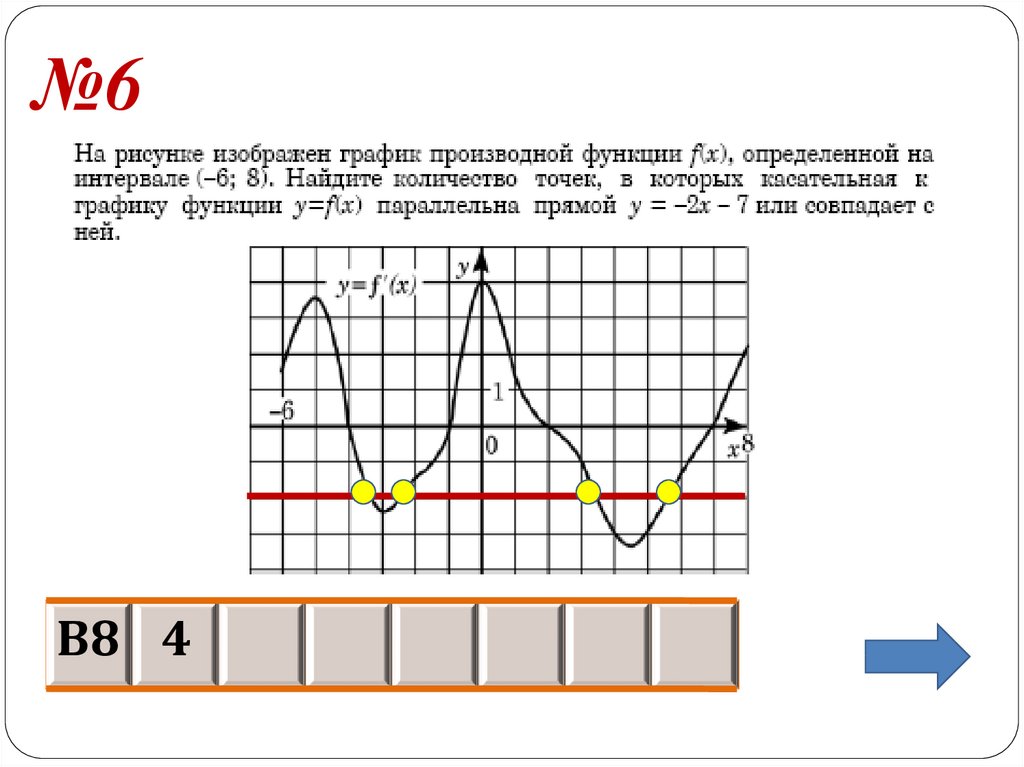
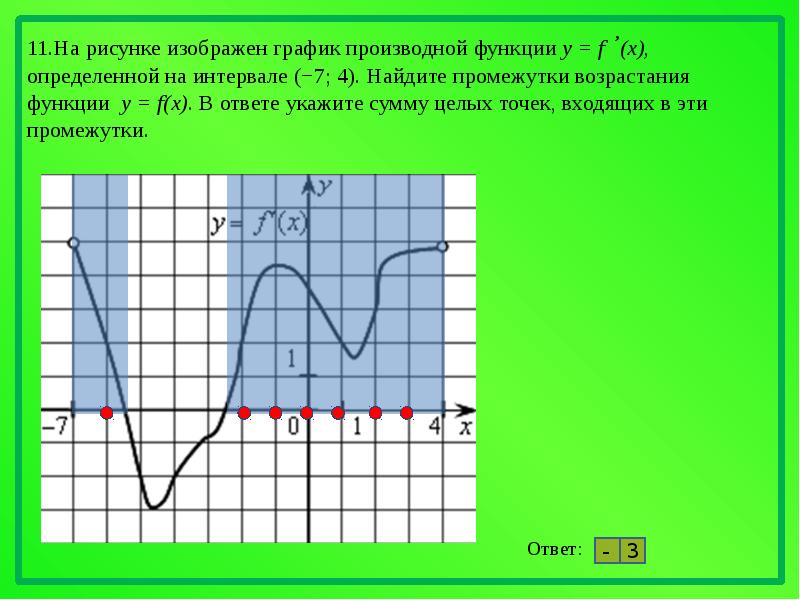
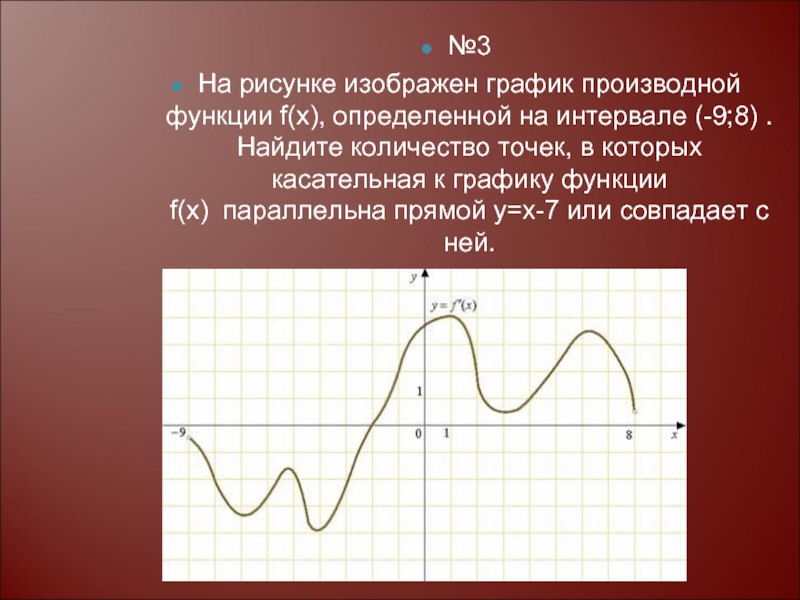
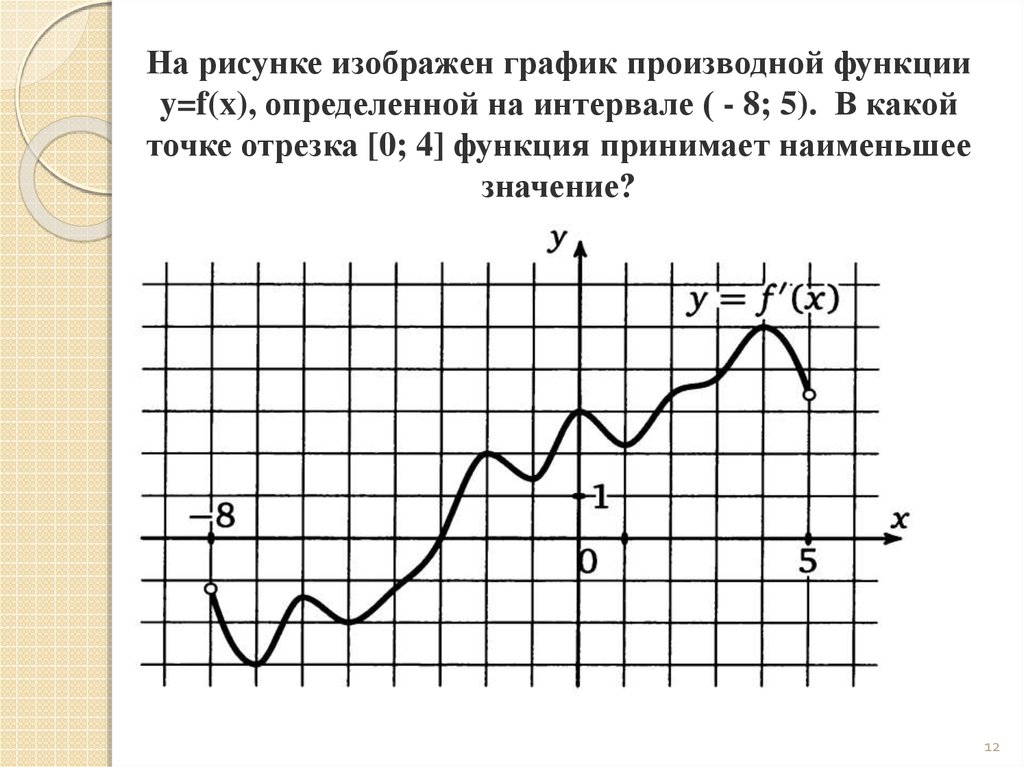
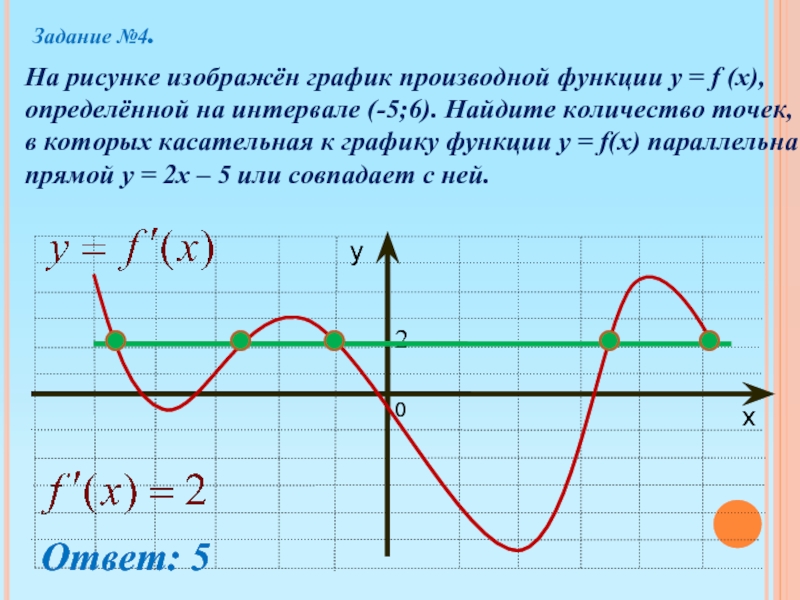
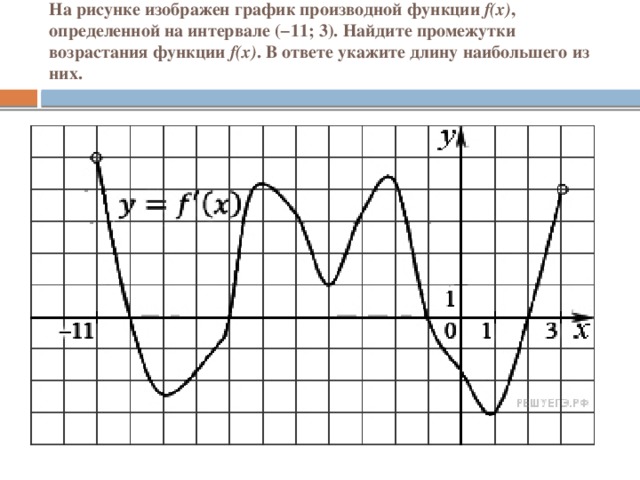
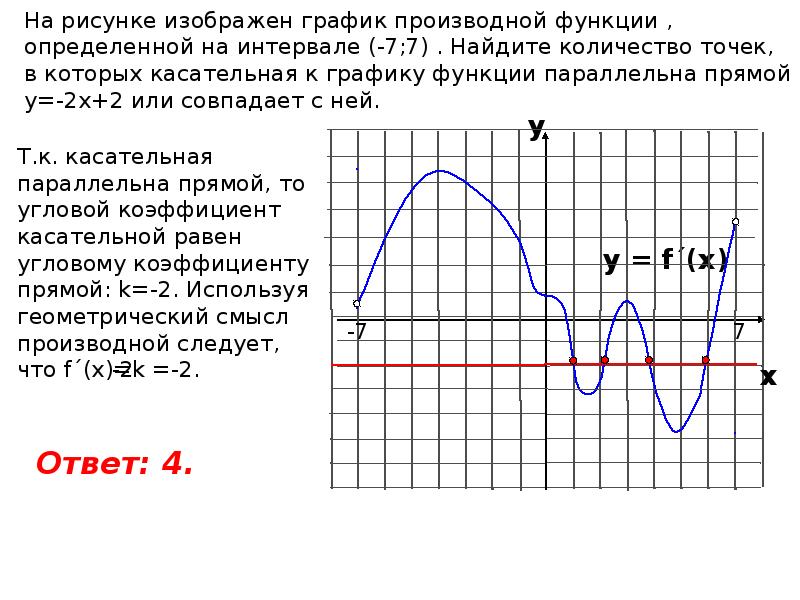
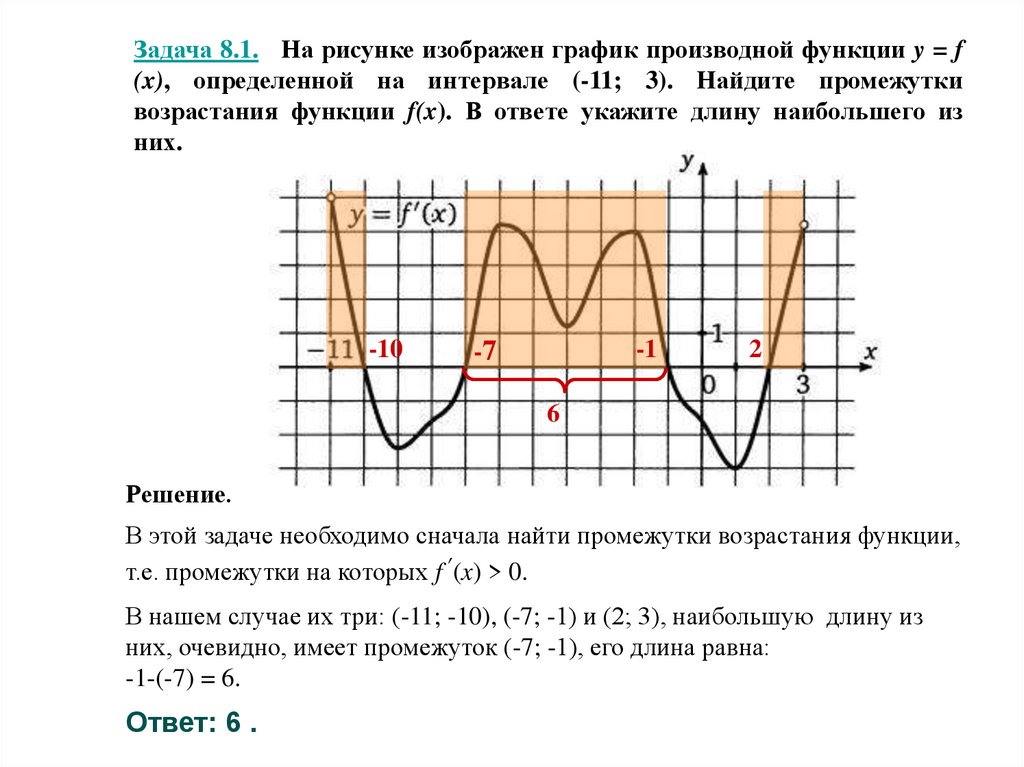
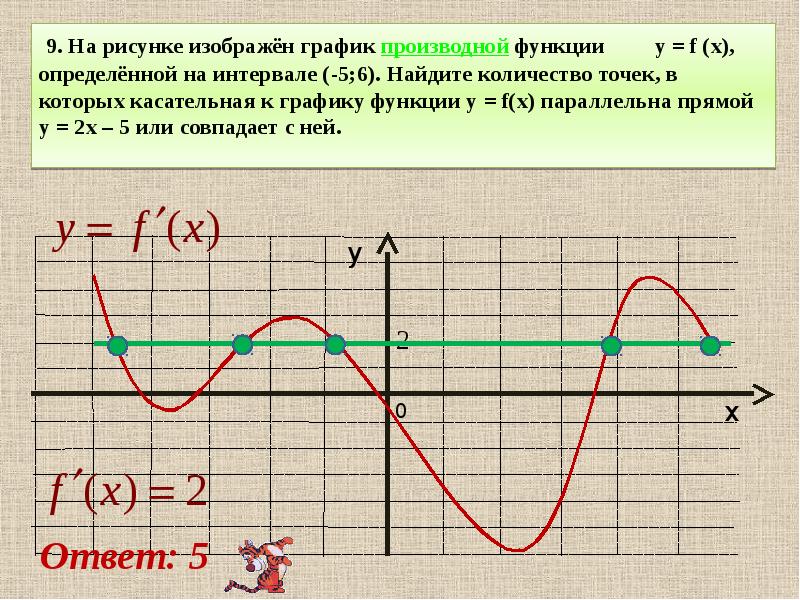
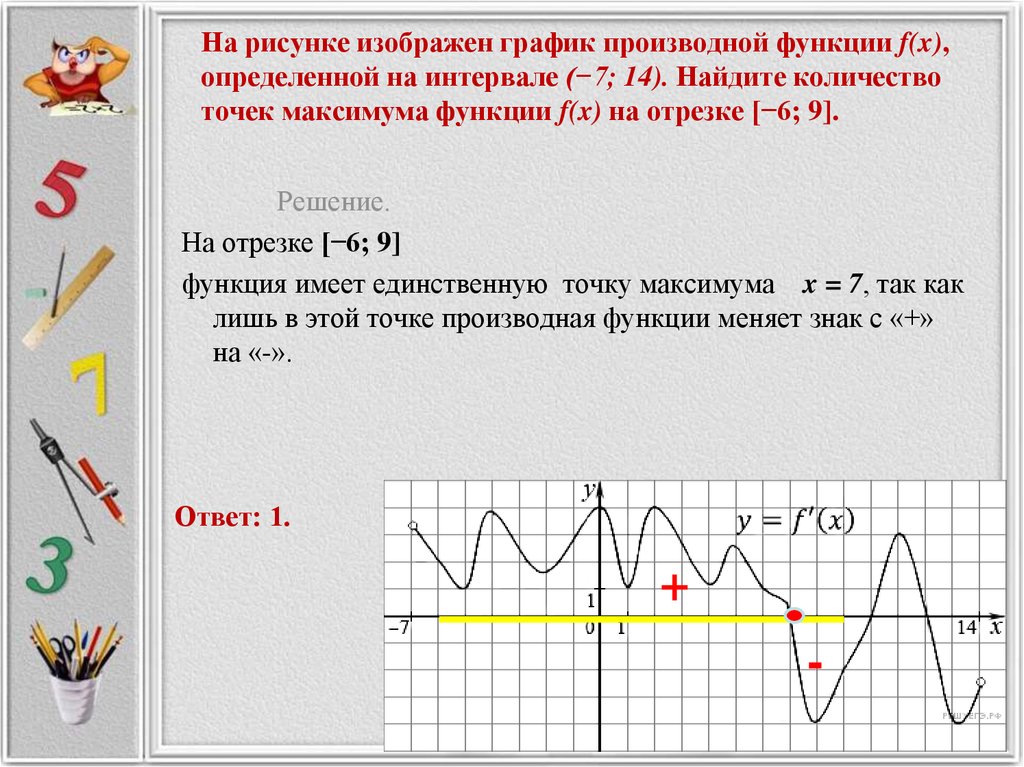
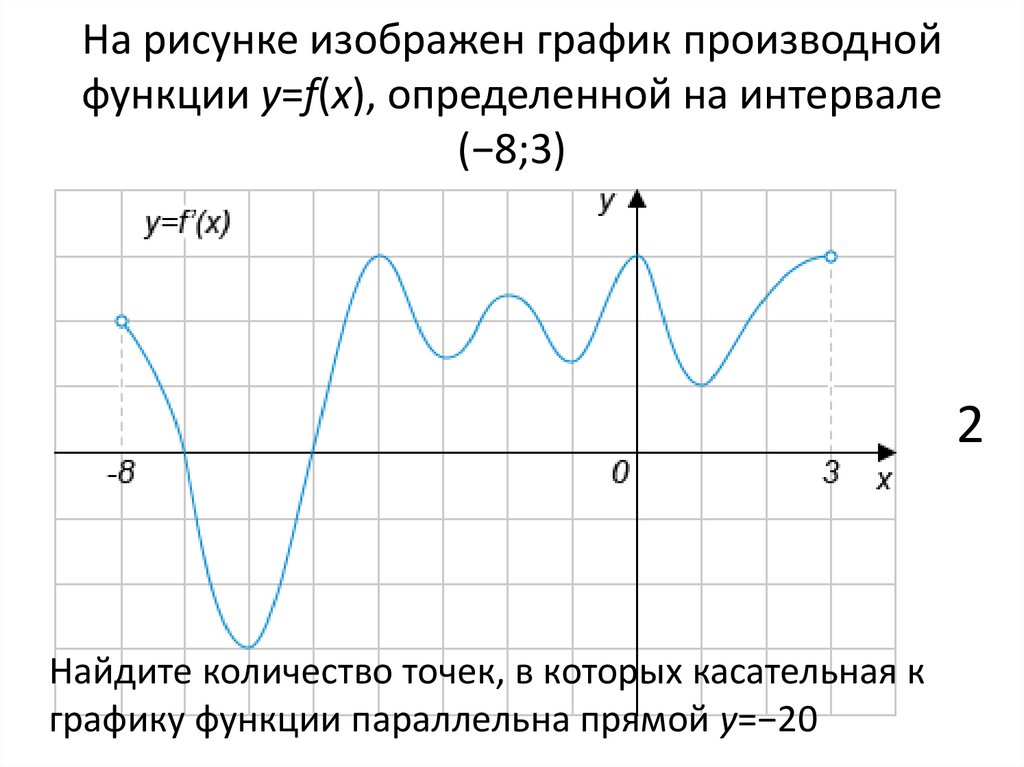
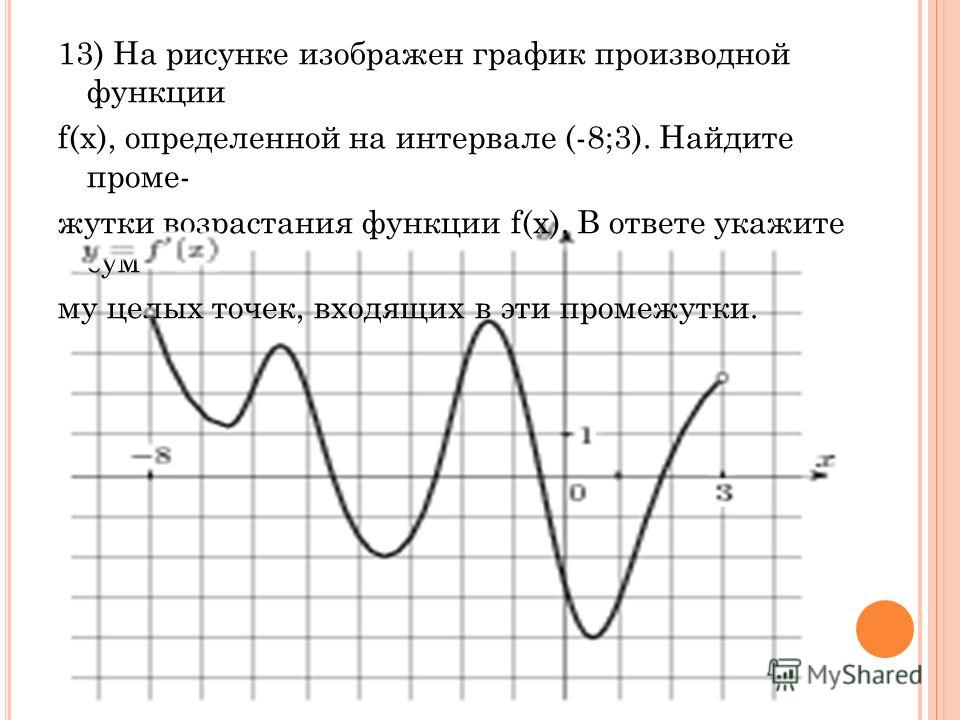
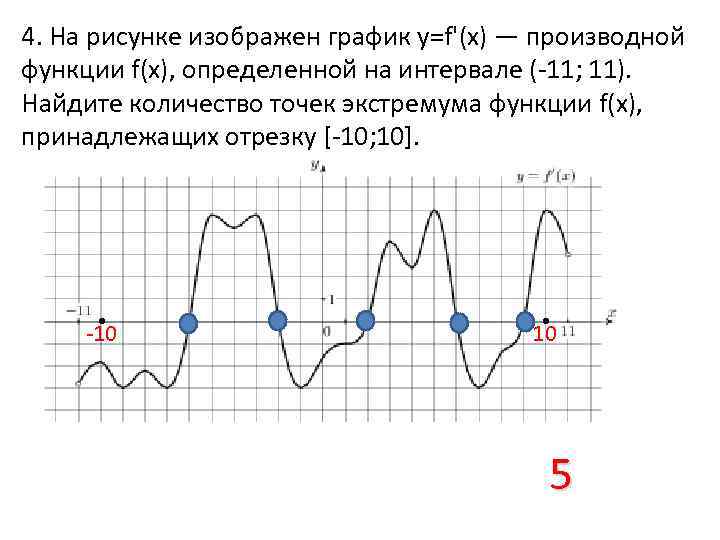
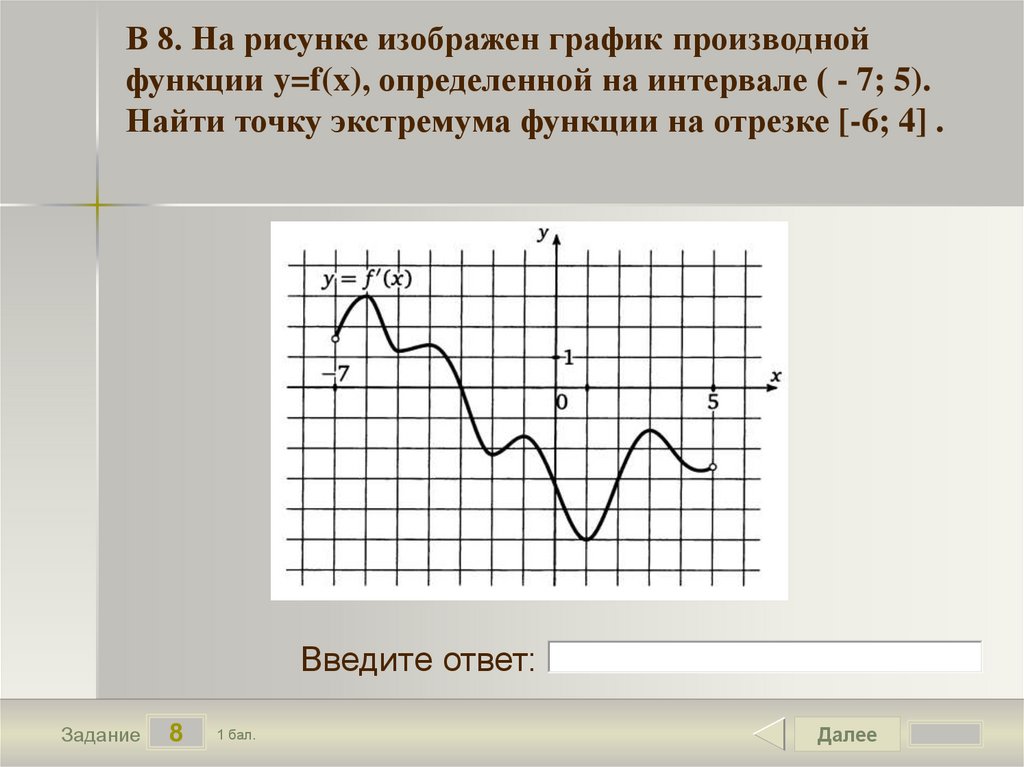
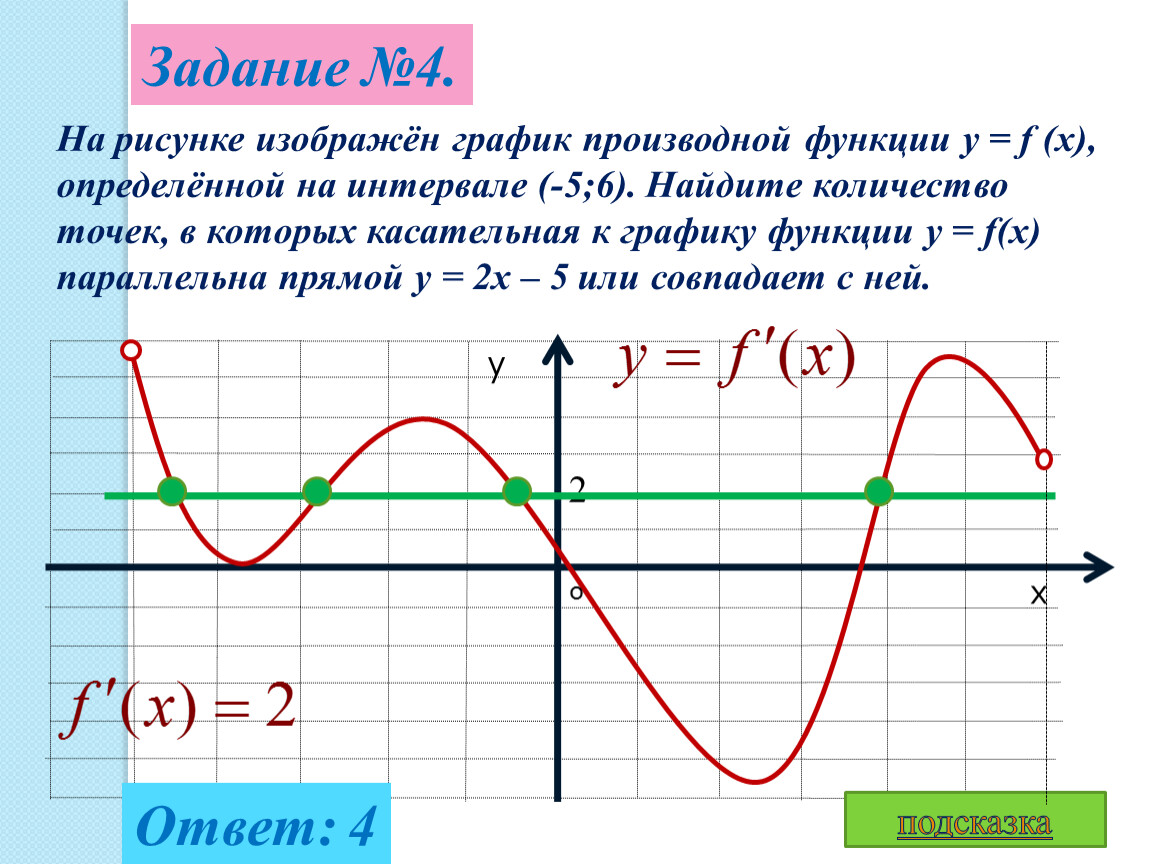
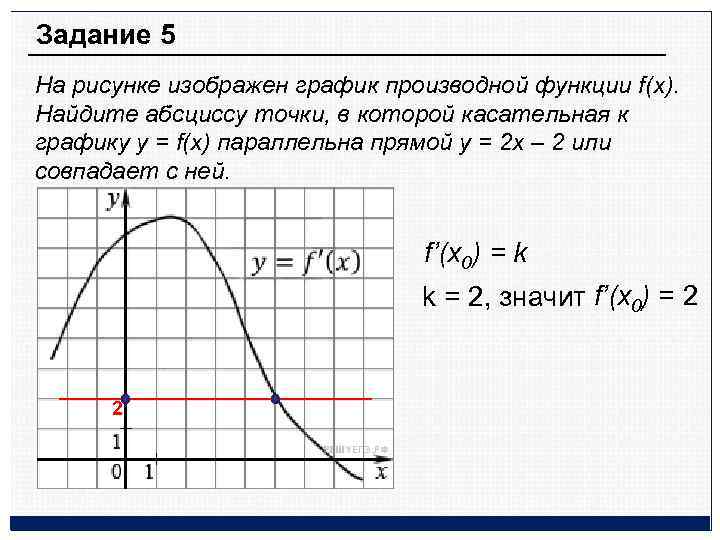
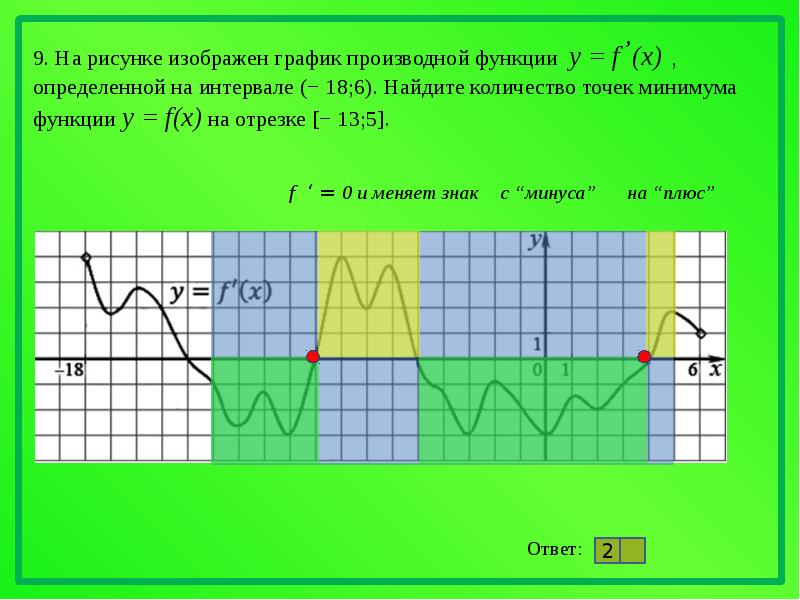
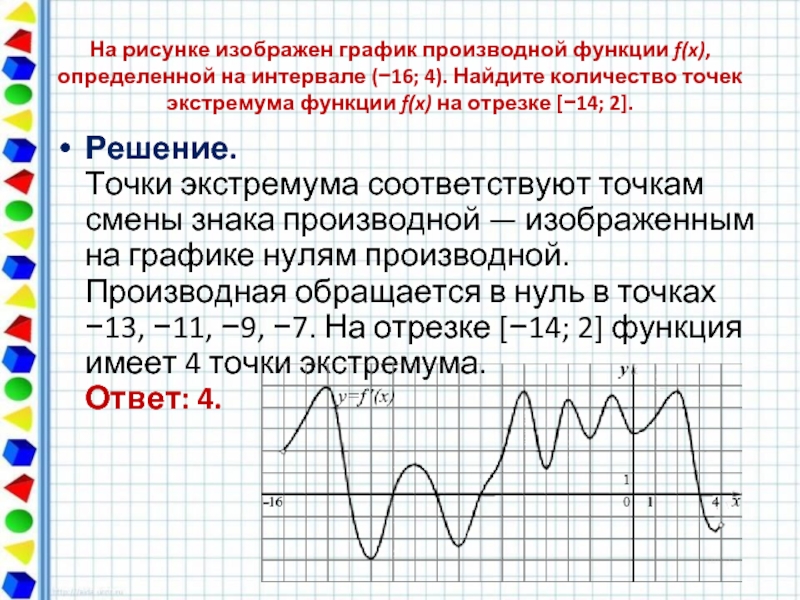
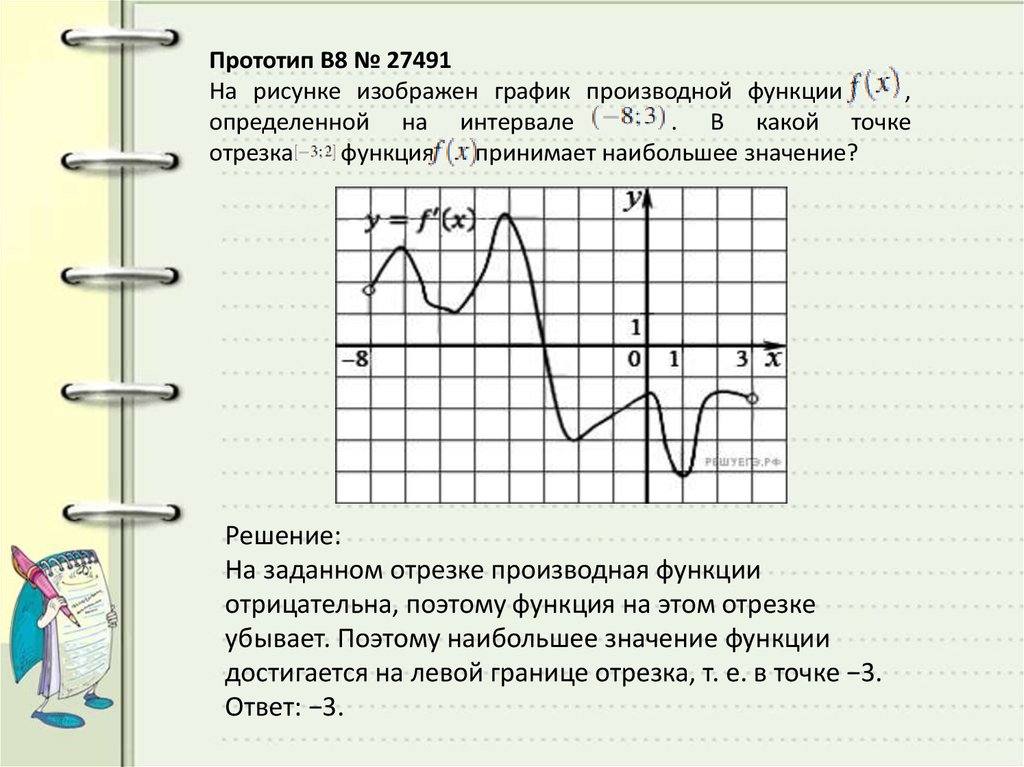
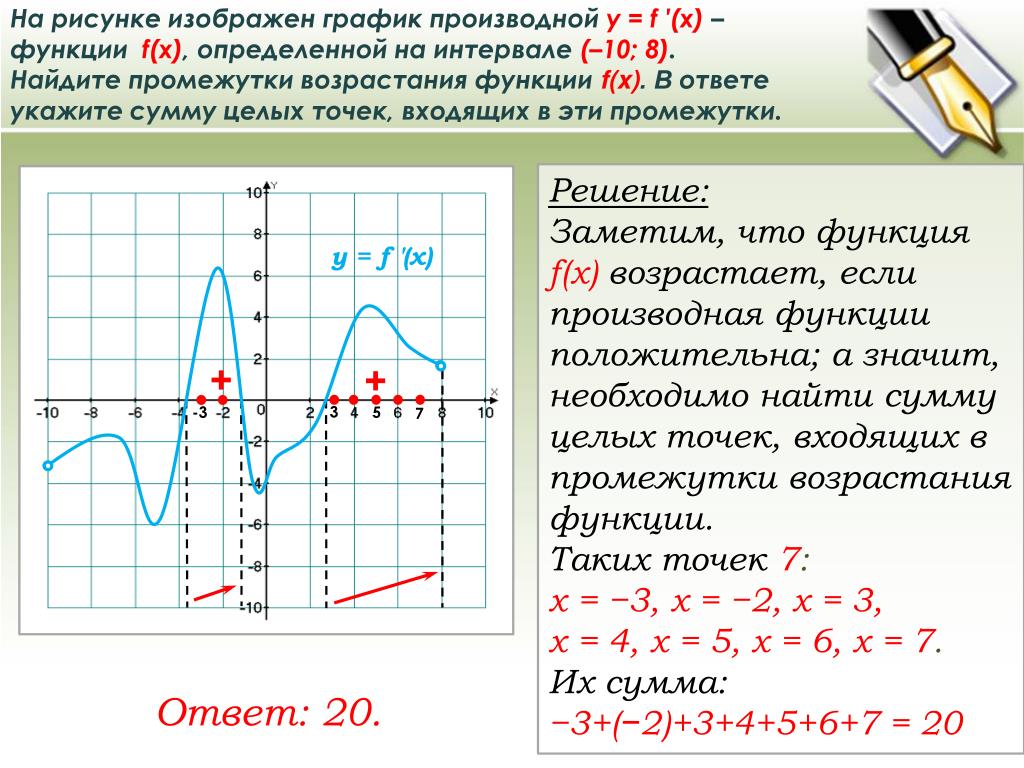
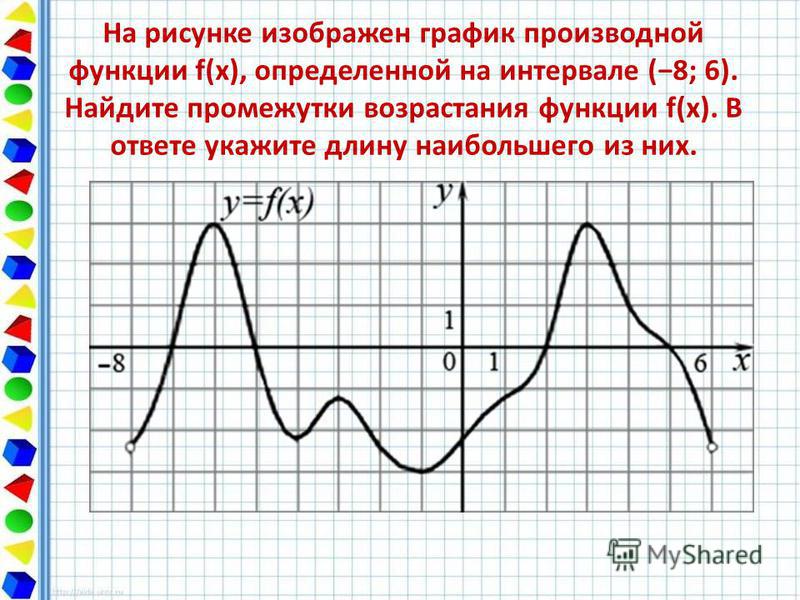
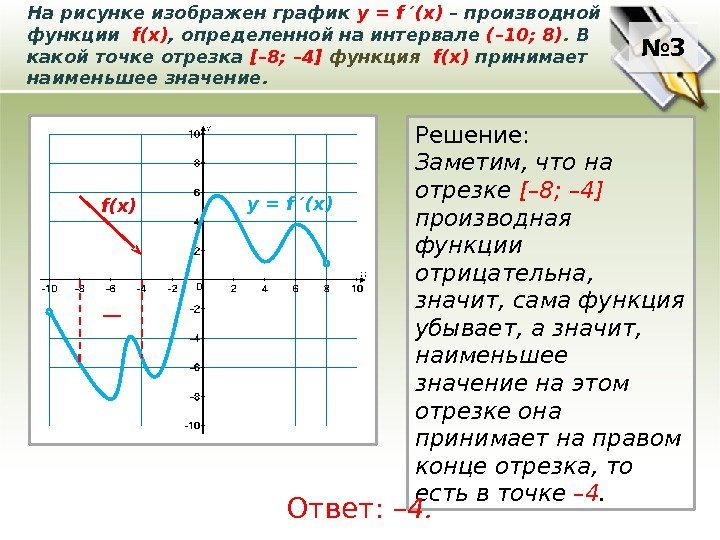
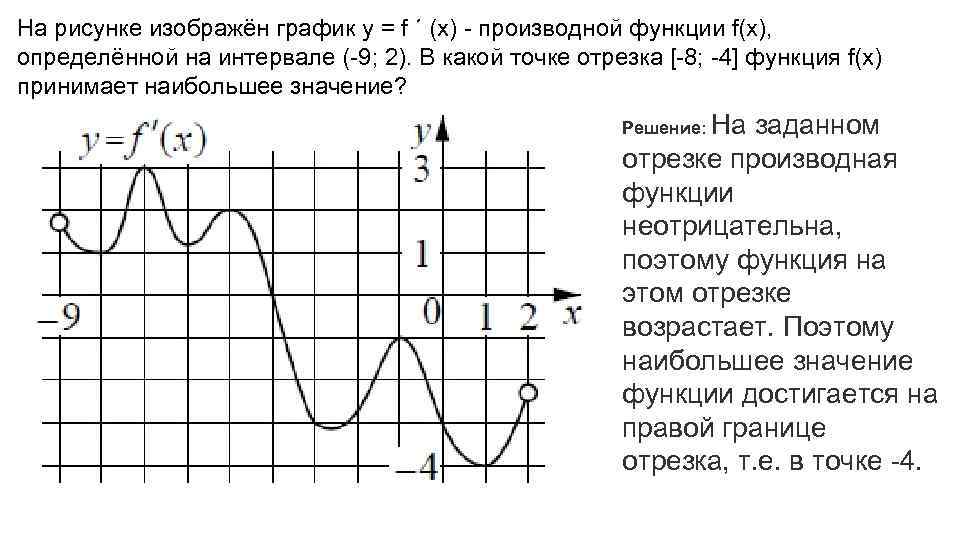
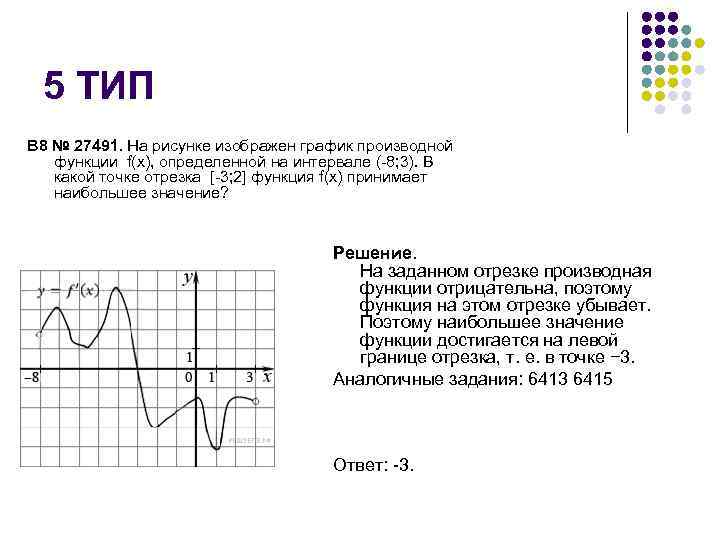
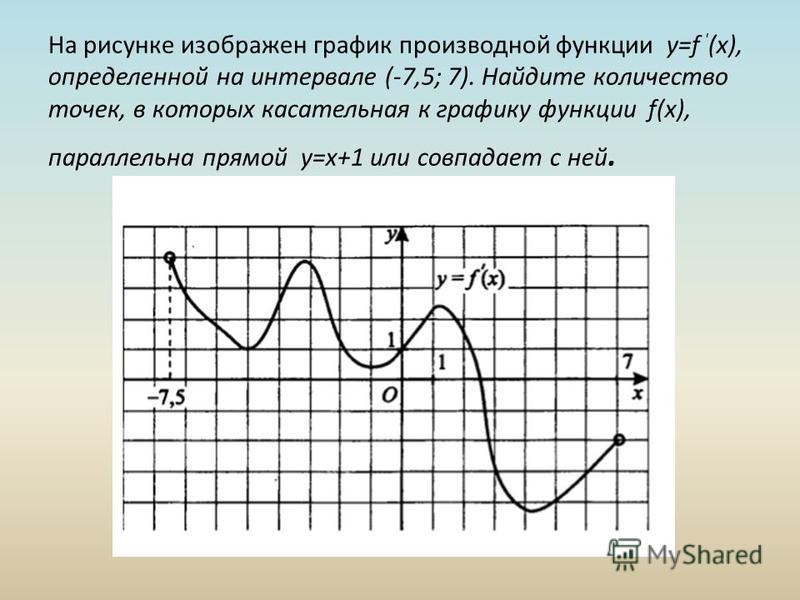
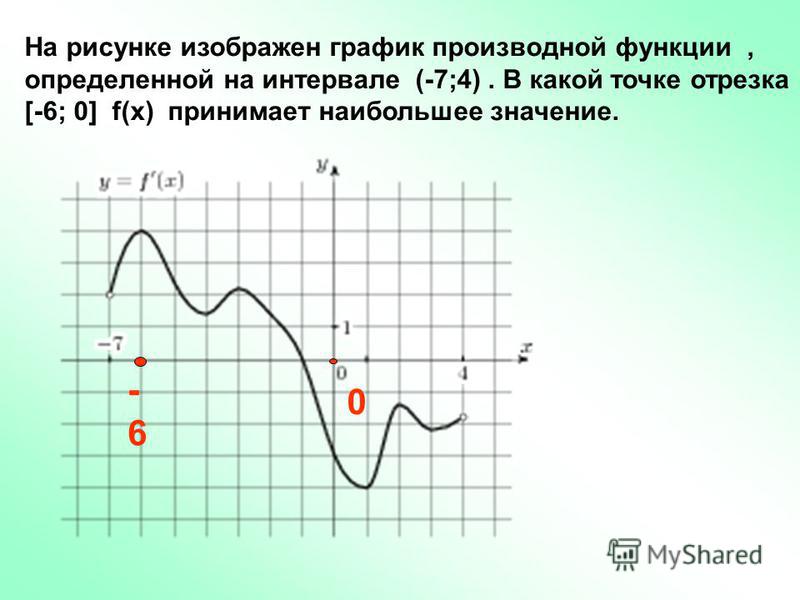
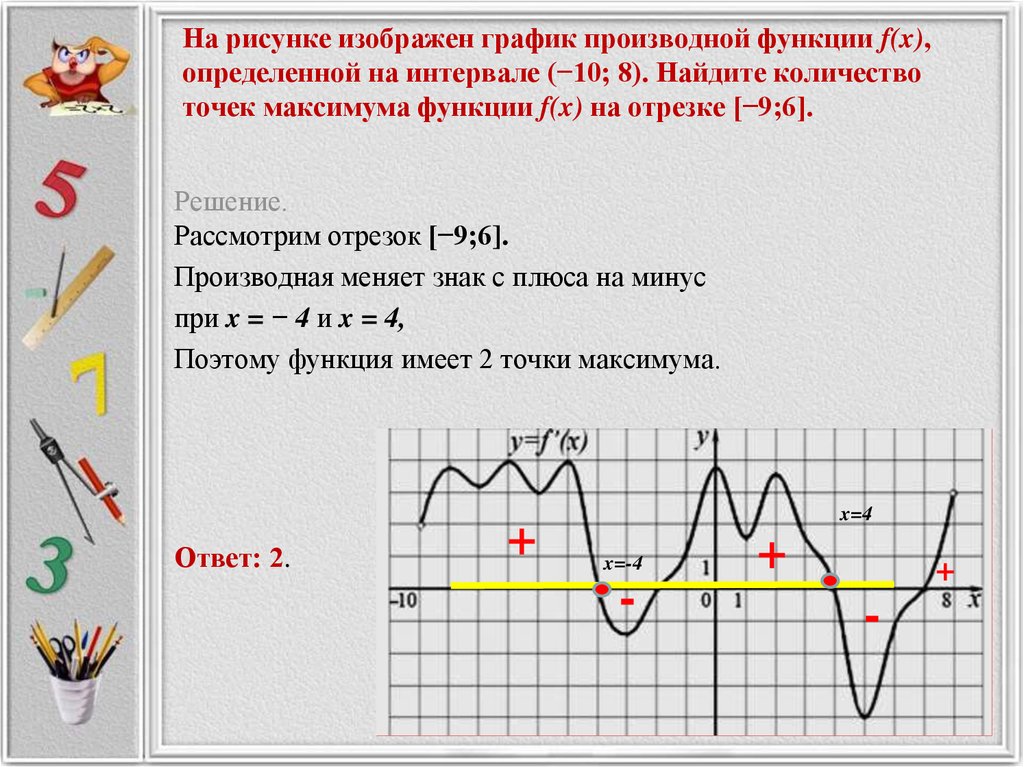
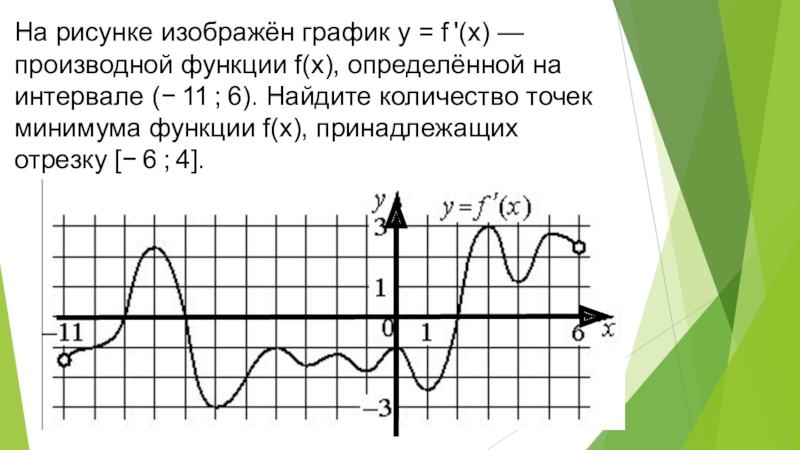
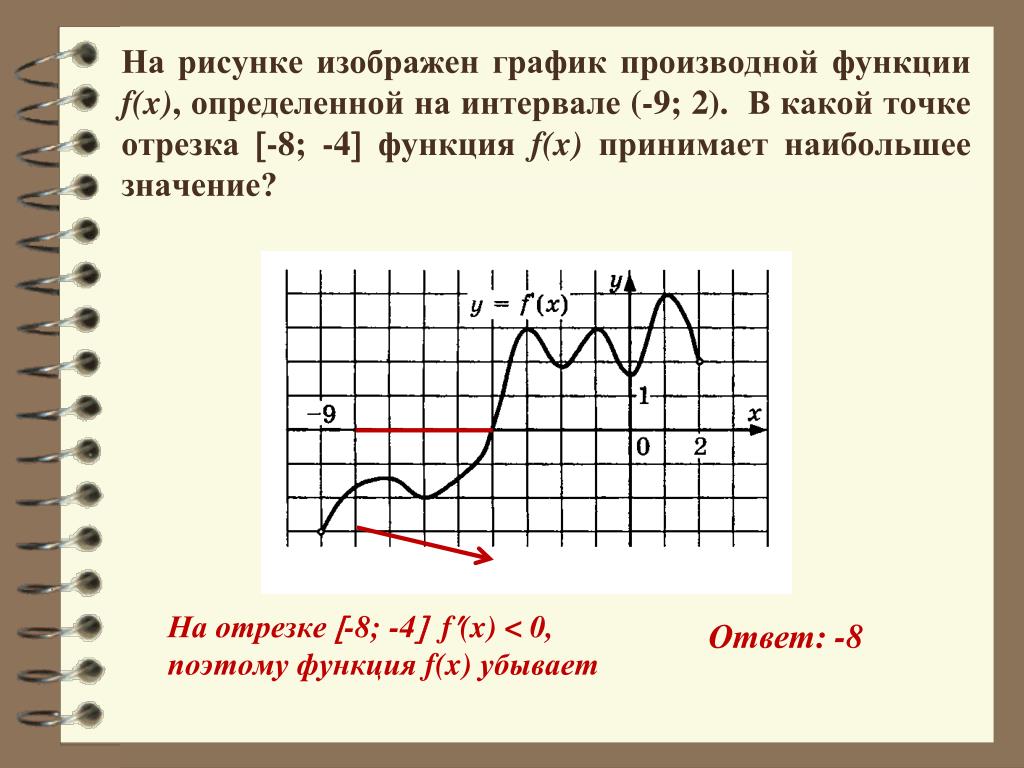
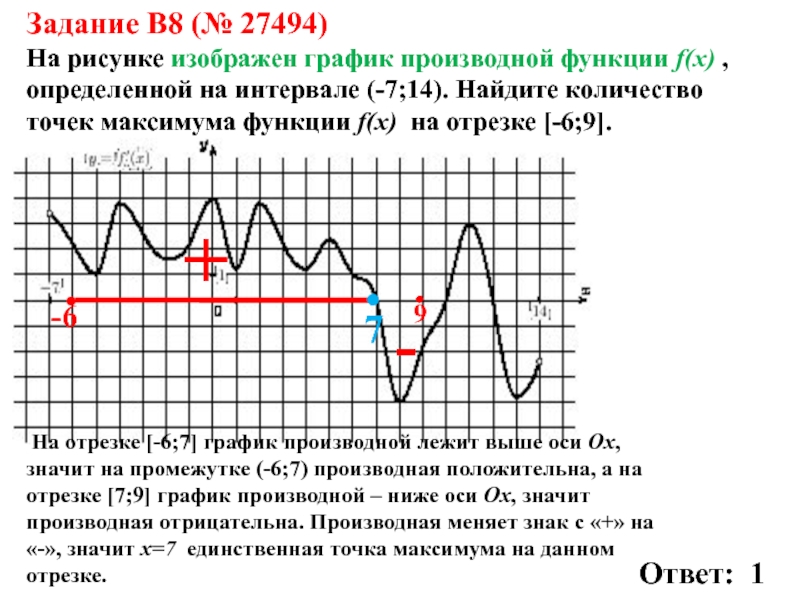
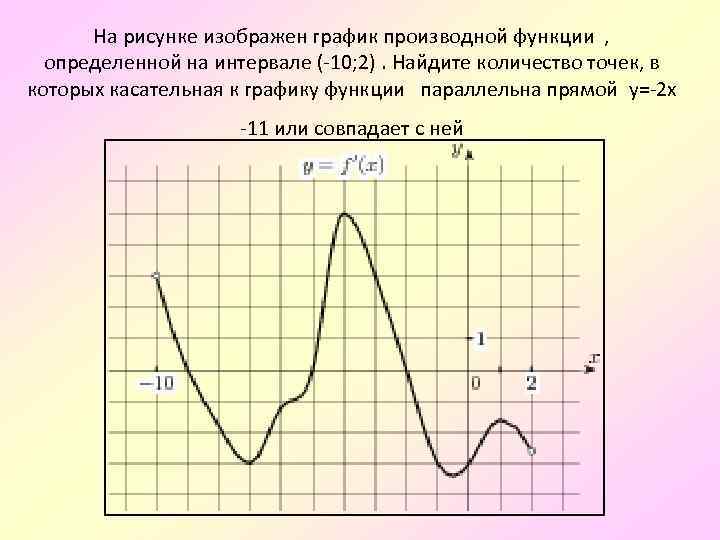
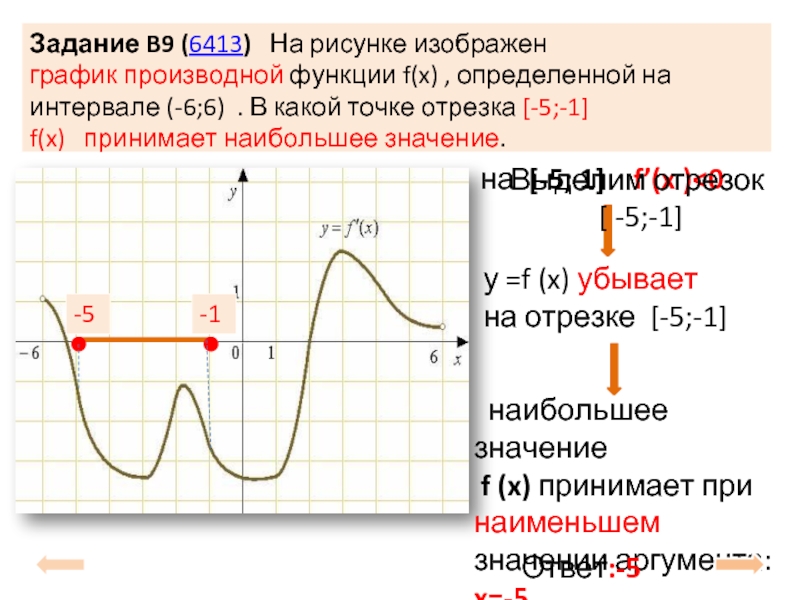
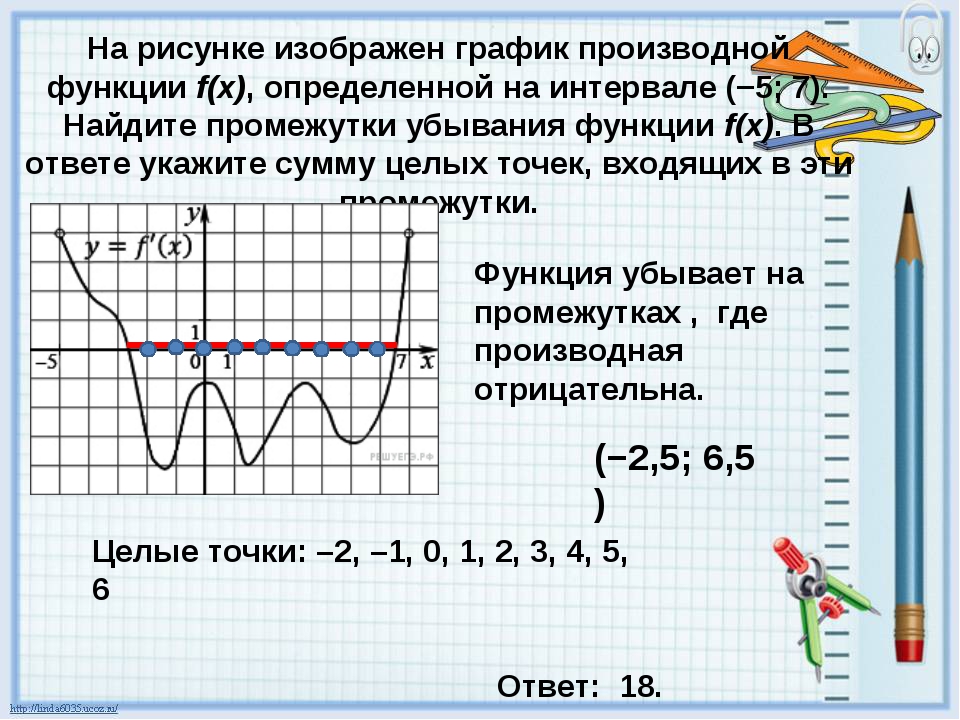
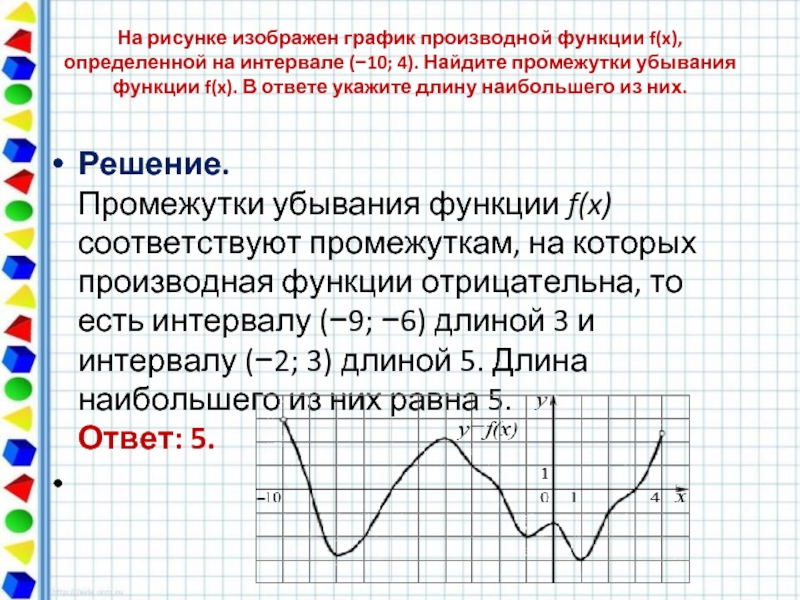
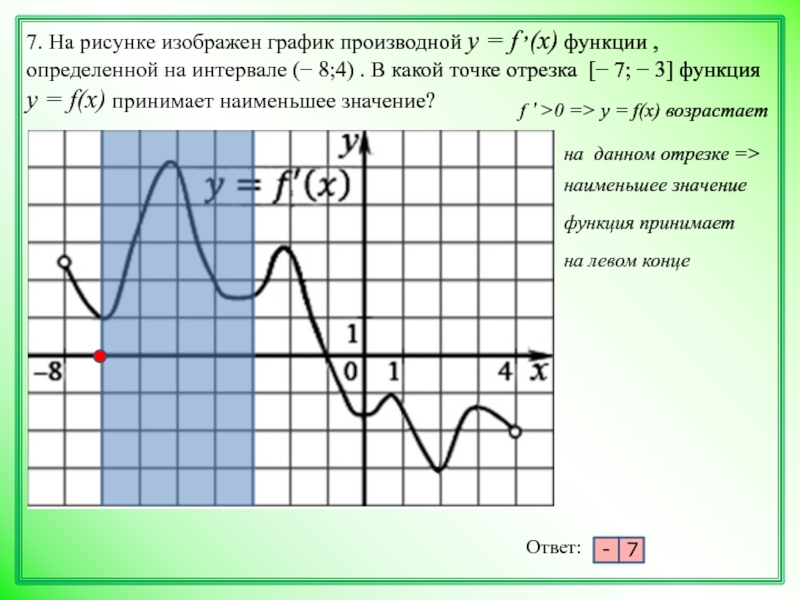
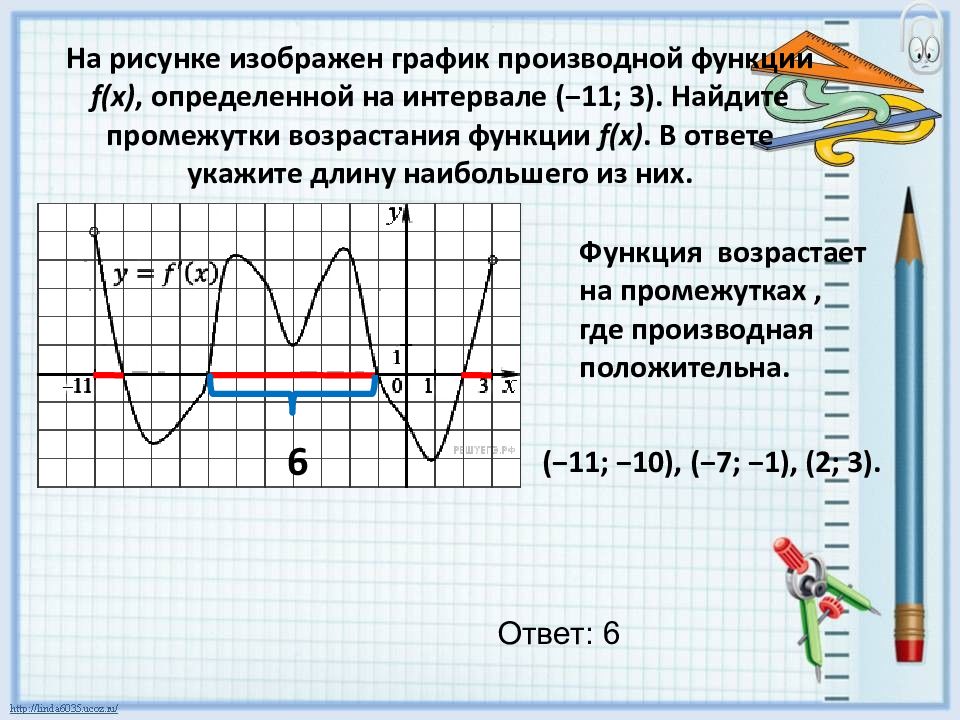
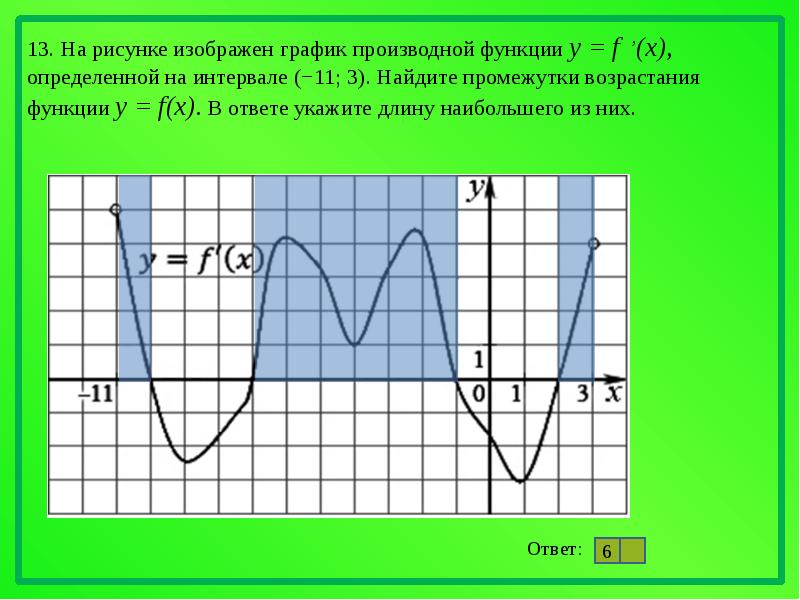
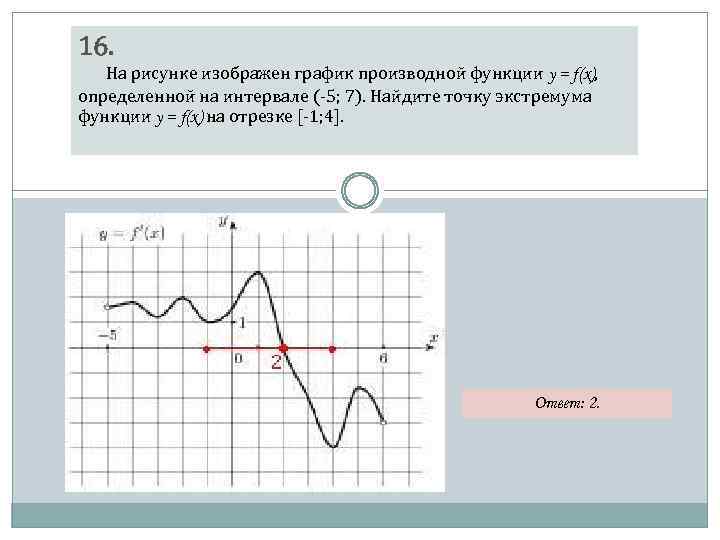
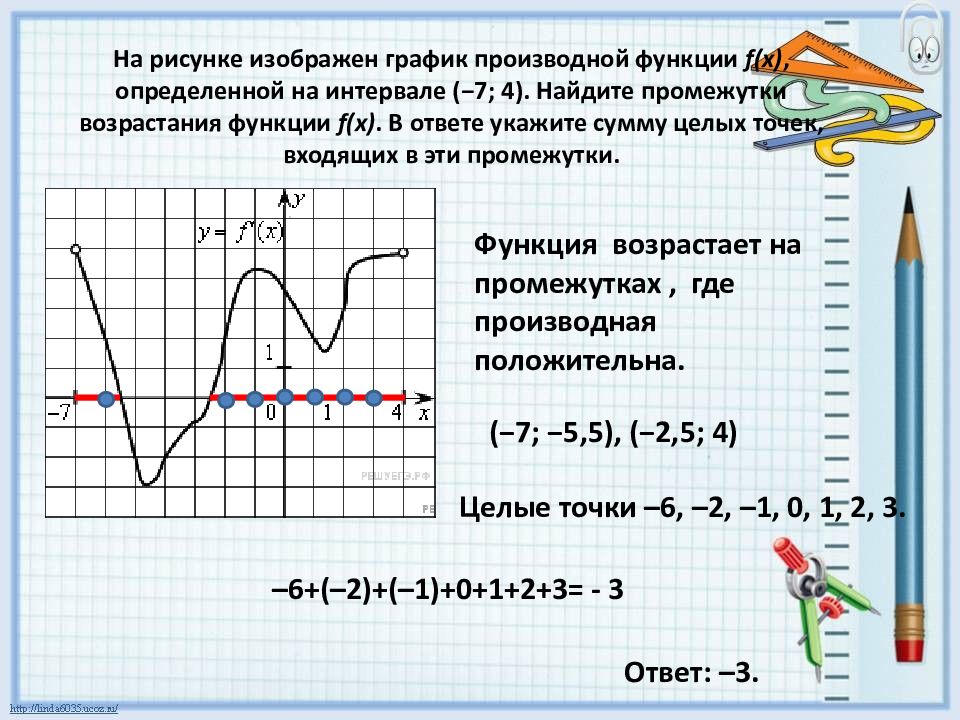
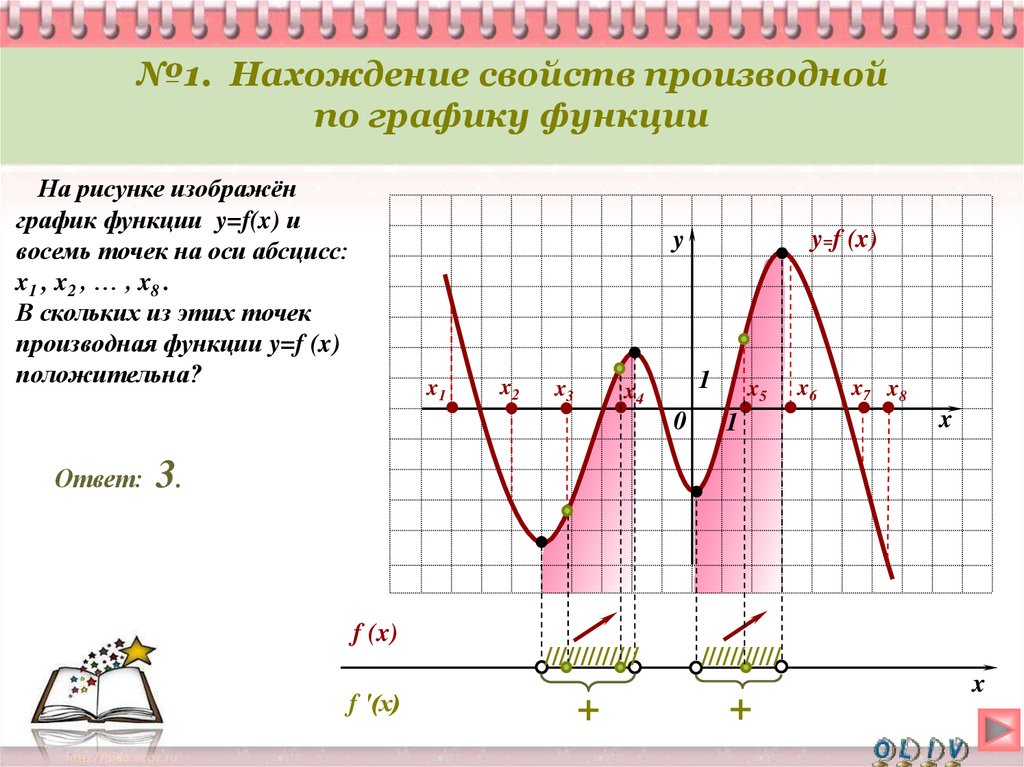
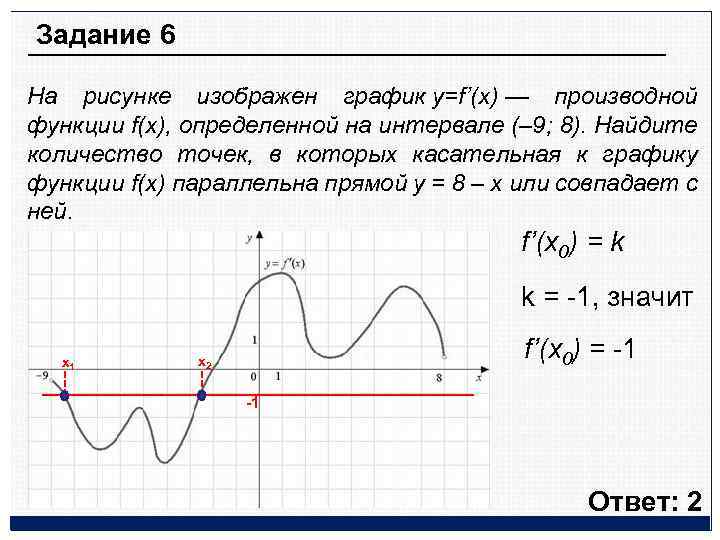
Функция f x определена на промежутке [-6 6] на рисунке изображен график.. Найдите промежутки возрастания функции график производной функции. График функции f(x), определенной на интервале (-6; 6).. Промежутки возрастания функции в ответ укажите сумму целых точек.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. График производной функции промежутки убывания. На рисунке график производной функции определенной на интервале. Промежутки убывания функции f x. На рисунке изображен график производной функции.
График производной функции промежутки убывания. На рисунке график производной функции определенной на интервале. Промежутки убывания функции f x. На рисунке изображен график производной функции.
На рисунке график производной функции. Количество точек минимума функции. Найдите количество точек минимума функции. Найдите количество точек минимума функции f x. Как найти количество точек минимума.
Количество точек минимума функции. Найдите количество точек минимума функции. Найдите количество точек минимума функции f x. Как найти количество точек минимума.
На рисунке график производной функции. Количество точек в которых касательная к графику параллельна прямой. Точки в которых касательная к графику функции параллельна прямой. Касательная к графику функции параллельна. Количество точек в которых касательная к графику параллельна.
Количество точек в которых касательная к графику параллельна прямой. Точки в которых касательная к графику функции параллельна прямой. Касательная к графику функции параллельна. Количество точек в которых касательная к графику параллельна.
На рисунке график производной функции
На рисунке график производной функции. На рисунке изображен график производной функции f. На рисунке график производной функции определенной на интервале. На рисунке изображен график производной функции f x -3 2. На рисунке изображён график функции y f x производной функции f x -11 2.
На рисунке изображен график производной функции f. На рисунке график производной функции определенной на интервале. На рисунке изображен график производной функции f x -3 2. На рисунке изображён график функции y f x производной функции f x -11 2.
На рисунке график производной функции. На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. На рисунке изображён график функции y f x производной функции f x -8 3. На рисунке изображен график производной функции f x на интервале -8 3.
На рисунке изображен график производной функции. На рисунке изображен график производной функции f x. На рисунке изображён график функции y f x производной функции f x -8 3. На рисунке изображен график производной функции f x на интервале -8 3.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. На рисунке изображен график производной. График производной функции y=f(x). На рисунке изображён график y f x производной функции f x. На рисунке изображен график производной функции f x.
На рисунке изображен график производной. График производной функции y=f(x). На рисунке изображён график y f x производной функции f x. На рисунке изображен график производной функции f x.
На рисунке график производной функции. Промежутки возрастания функции на графике производной. На рисунке изображен график функции определенной на интервале -5 5. Функция убывает на рисунке. На рисунке изображен график функции определенной на интервале -5 7.
Промежутки возрастания функции на графике производной. На рисунке изображен график функции определенной на интервале -5 5. Функция убывает на рисунке. На рисунке изображен график функции определенной на интервале -5 7.
На рисунке график производной функции. Точки экстремума функции на графике производной. Точки экстремума на графике производной. Точки экстремума производной функции. Знак производной на графике.
Точки экстремума функции на графике производной. Точки экстремума на графике производной. Точки экстремума производной функции. Знак производной на графике.
На рисунке график производной функции
На рисунке график производной функции. Точки максимума Графика производной функции. График производной максимум функции. Точки максимума на графике производной. Максимум функции на графике производной.
Точки максимума Графика производной функции. График производной максимум функции. Точки максимума на графике производной. Максимум функции на графике производной.
На рисунке график производной функции
На рисунке график производной функции. График производной и график функции. Производная функции график. Таблица график производной. Виды графиков производных.
График производной и график функции. Производная функции график. Таблица график производной. Виды графиков производных.
На рисунке график производной функции. График производной. График производной функции. Функция и производная на графике. Графики производной и функции.
График производной. График производной функции. Функция и производная на графике. Графики производной и функции.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. График производной знаки. Как определить знаки производной функции на рисунке. Решения уравнения график производной. Определить знак производной по графику функции.
График производной знаки. Как определить знаки производной функции на рисунке. Решения уравнения график производной. Определить знак производной по графику функции.
На рисунке график производной функции. Найдите Кол-во точек минимума функции. Найти количество точек минимума функции. Найдите количество точек минимума функции. Найтиколисчестиво точек минимума.
Найдите Кол-во точек минимума функции. Найти количество точек минимума функции. Найдите количество точек минимума функции. Найтиколисчестиво точек минимума.
На рисунке график производной функции. Касательная к графику функции у х в точке х0. Найдите значение производной функции в точке. Нахождение производной по графику функции и касательной. На рисунке изобрахён график ф.
Касательная к графику функции у х в точке х0. Найдите значение производной функции в точке. Нахождение производной по графику функции и касательной. На рисунке изобрахён график ф.
На рисунке график производной функции. На рисунке изображен график производной функции f x на интервале -8 3. На рисунке изображен график производной функции y f x. На рисунке изображен график производной функции f x. График y = f '(x) — производной функции f(x).
На рисунке изображен график производной функции f x на интервале -8 3. На рисунке изображен график производной функции y f x. На рисунке изображен график производной функции f x. График y = f '(x) — производной функции f(x).
На рисунке график производной функции. Найти количество точек минимума функции производной на отрезке. Количество точек минимума функции. Найдите количество точек минимума функции. Точка минимума на промежутке.
Найти количество точек минимума функции производной на отрезке. Количество точек минимума функции. Найдите количество точек минимума функции. Точка минимума на промежутке.
На рисунке график производной функции
На рисунке график производной функции
На рисунке график производной функции. На рисунке изображен график производной функции. Промежутки убывания производной функции. График производной промежутки убывания. На рисунке изображен график производной функции f x.
На рисунке изображен график производной функции. Промежутки убывания производной функции. График производной промежутки убывания. На рисунке изображен график производной функции f x.

Leave a Comment

Your email address will not be published. Required fields are marked *