Y f x 1 на рисунке

By /

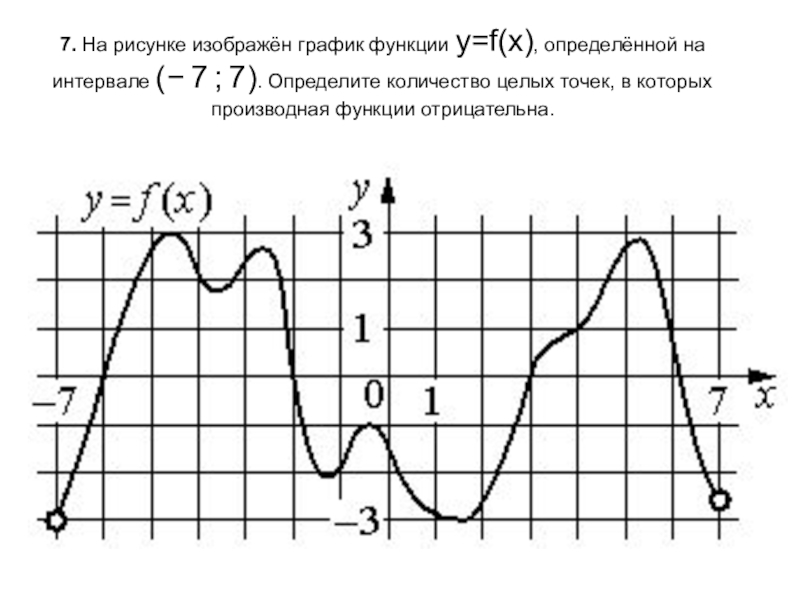
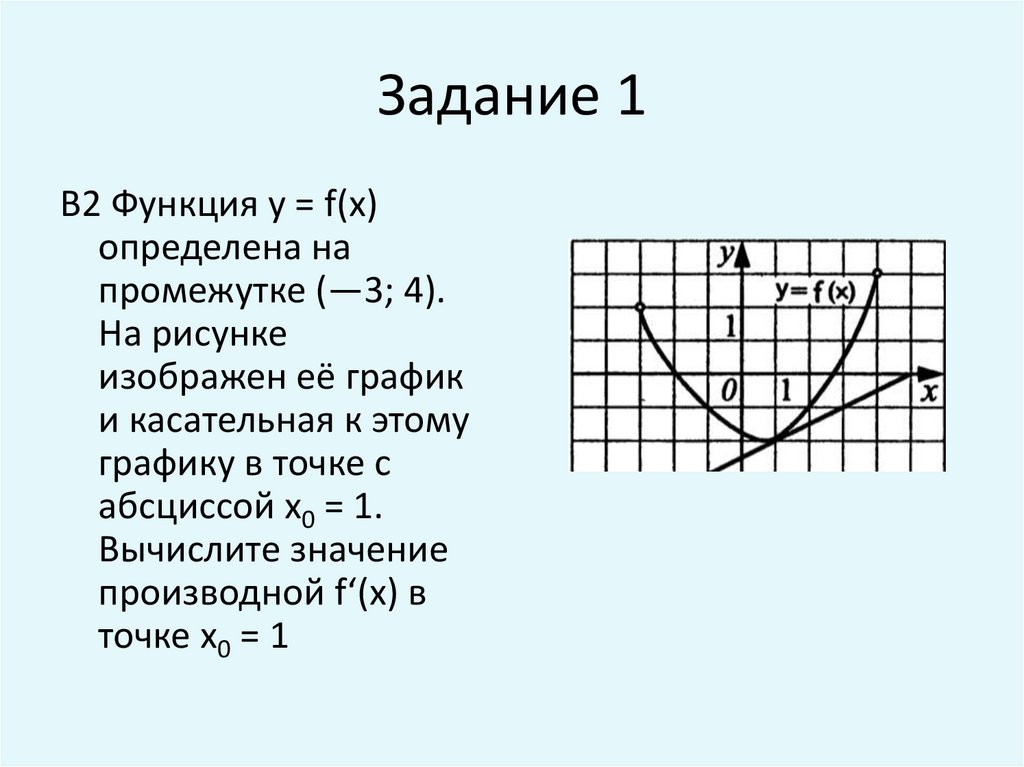
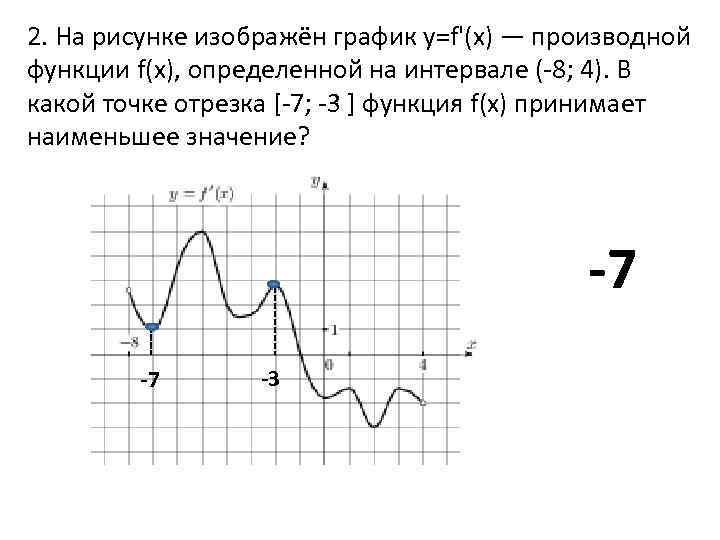
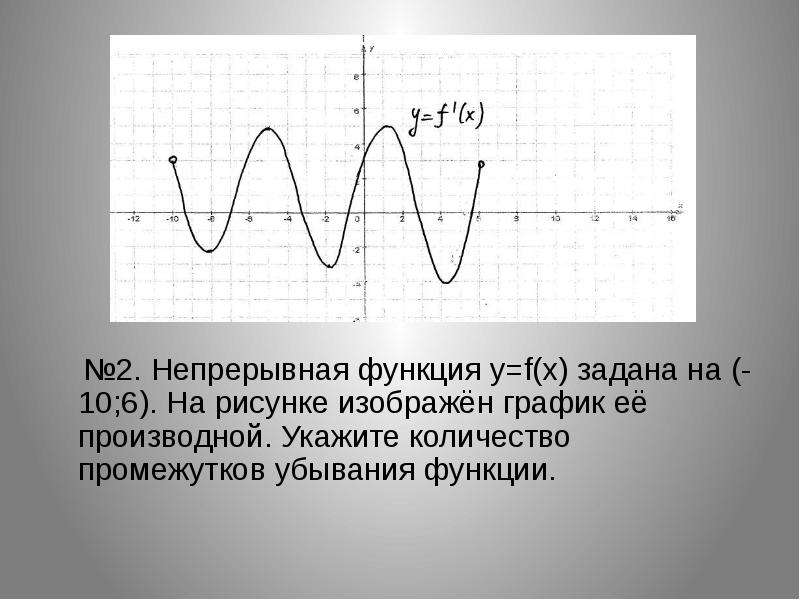
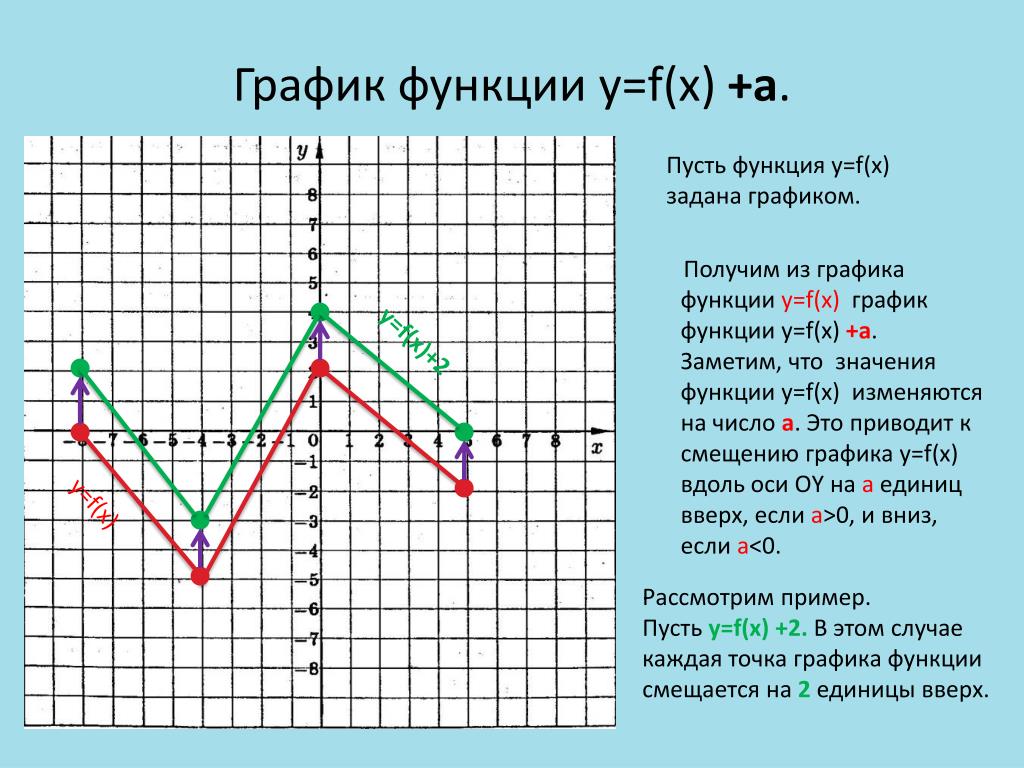
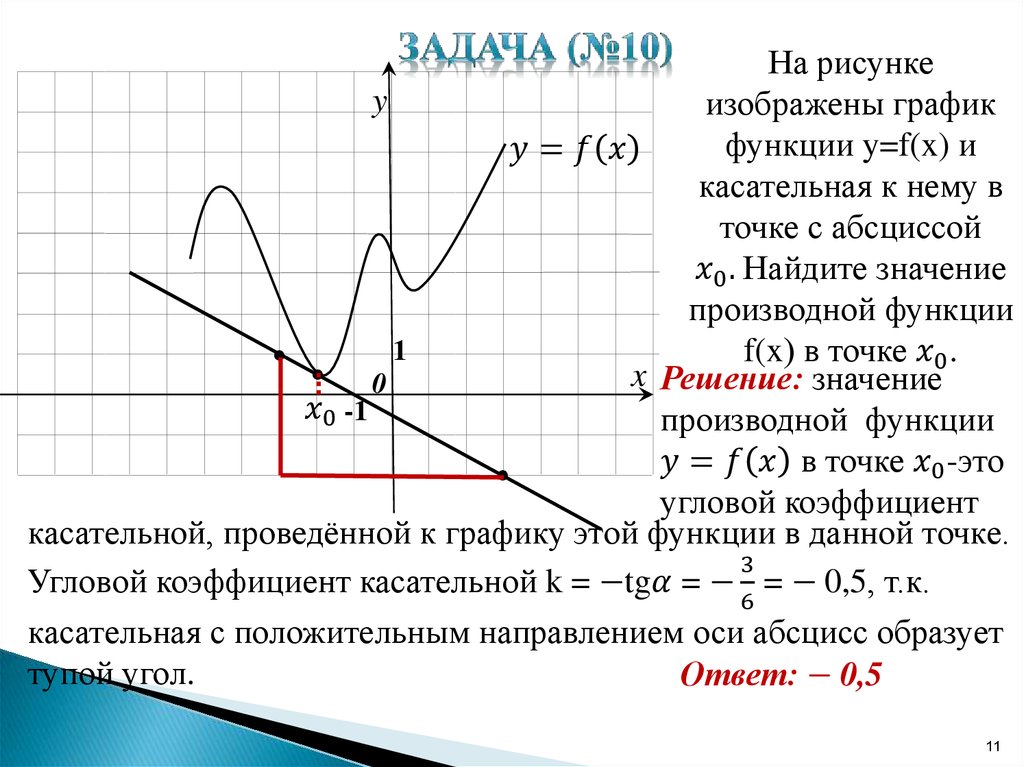
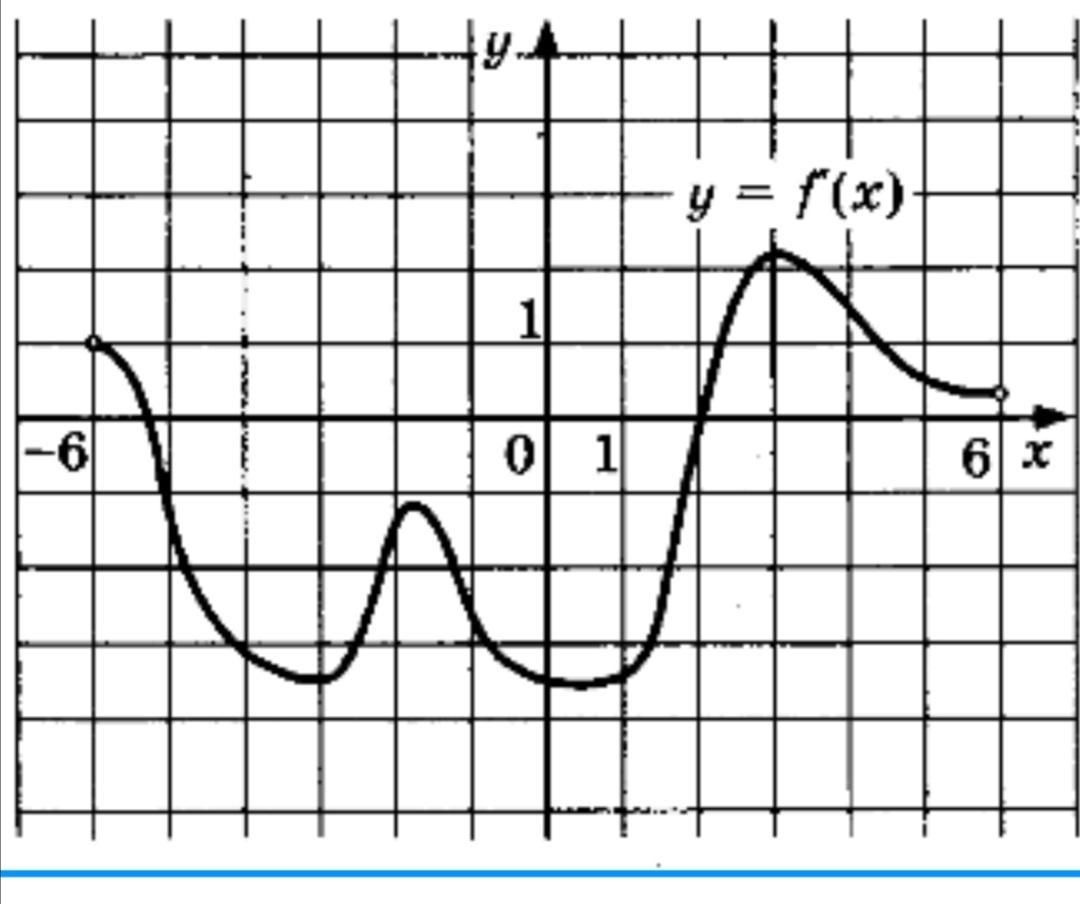
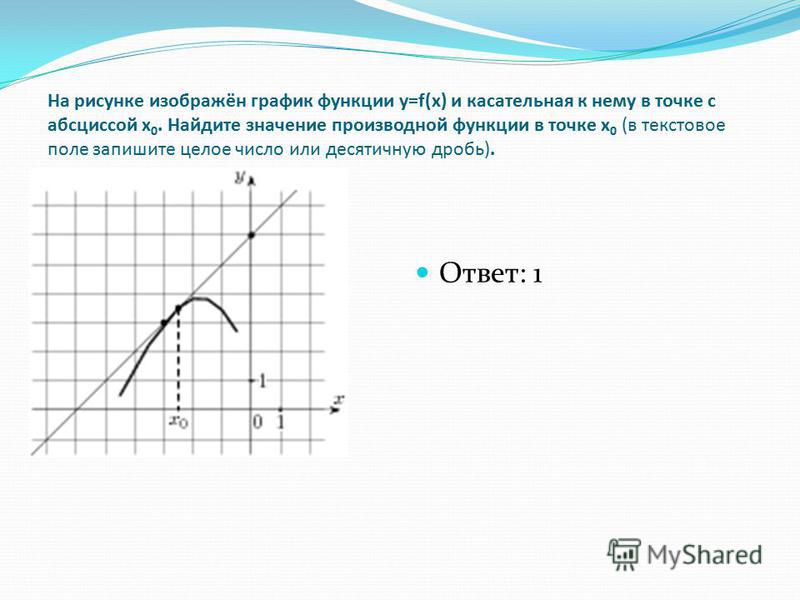
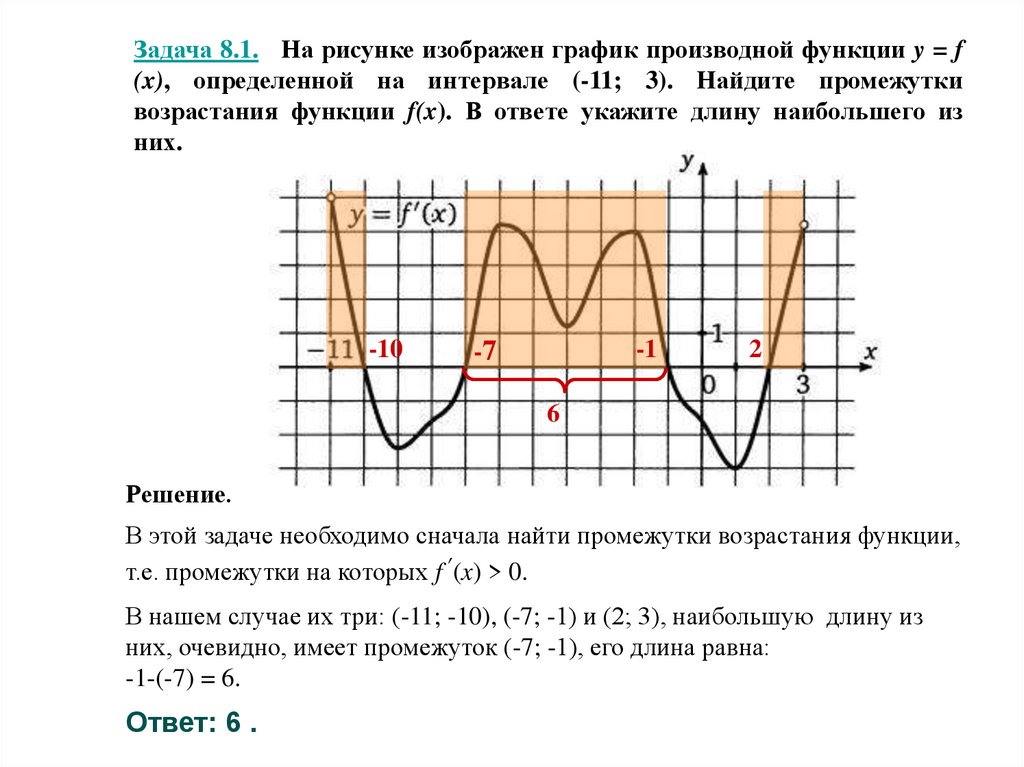
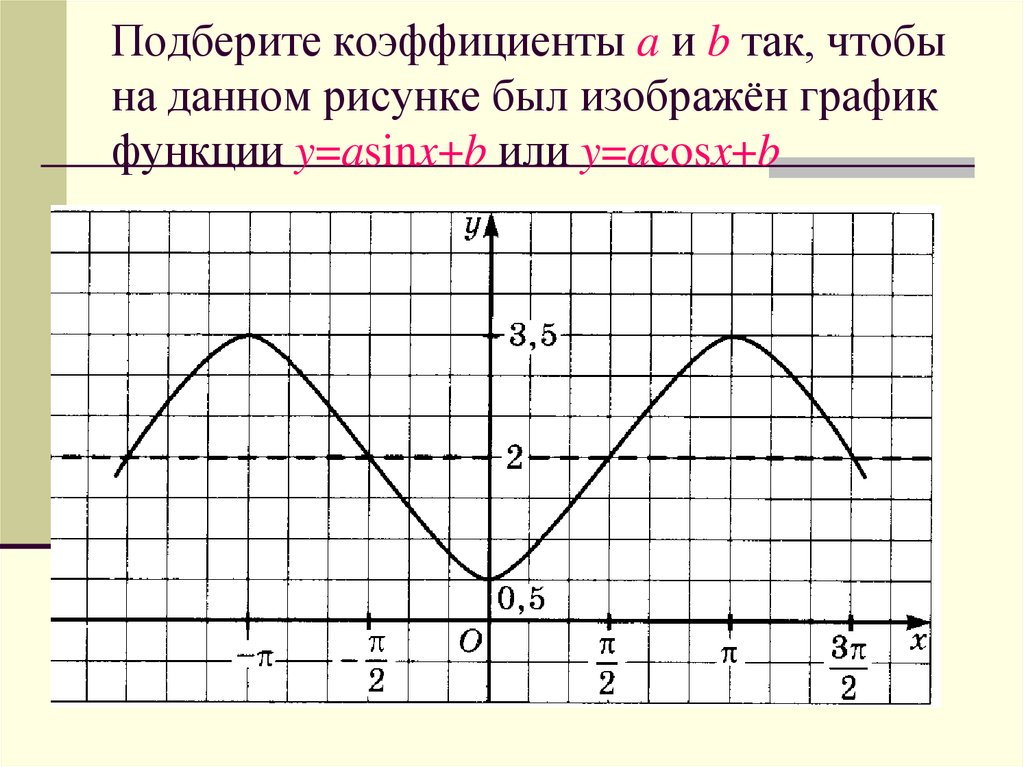
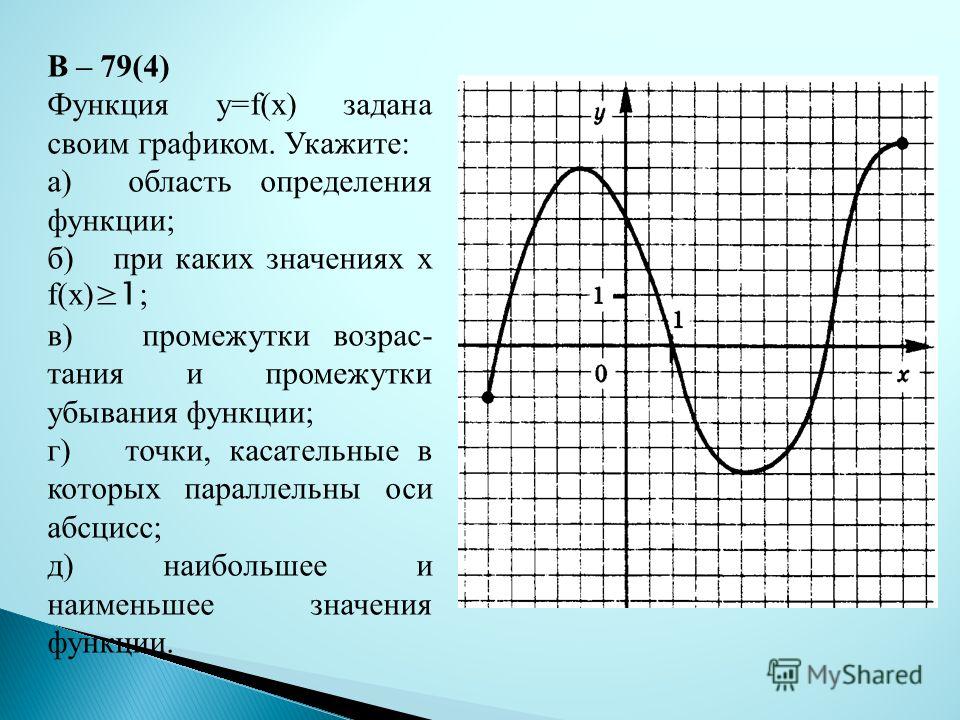
В данной статье мы рассмотрим функцию \( y = f(x) + 1 \) и её графическое представление. Этот тип преобразования функции является одним из основных в математическом анализе и геометрии, позволяющим глубже понять изменения, происходящие с графиком функции при простых арифметических операциях. На рисунке мы увидим, как параллельный перенос вверх на единицу влияет на положение и форму исходного графика функции \( f(x) \), что имеет важное значение для решения задач в различных областях науки и техники.
Y f x 1 на рисунке

Y f x 1 на рисунке. Y FX график функции. Функция y f x. Y=F(X). График f(x).
Y FX график функции. Функция y f x. Y=F(X). График f(x).
Y f x 1 на рисунке. Y F X график. Функции рисунок. Изображение Графика функции. График f(x).
Y F X график. Функции рисунок. Изображение Графика функции. График f(x).
Y f x 1 на рисунке. Изобразите график mн. Найди значение производной функции y = sinx в точке x0=5pi/2.
Изобразите график mн. Найди значение производной функции y = sinx в точке x0=5pi/2.
Y f x 1 на рисунке
Y f x 1 на рисунке
Y f x 1 на рисунке. Пеивообрвщнвя функции на интервале. На рисунке изображён график функции y f cos пи x BC D.
Пеивообрвщнвя функции на интервале. На рисунке изображён график функции y f cos пи x BC D.
Y f x 1 на рисунке. График функции. Графические функции. Произвольные графики функций. Что такое к в графике функций.
График функции. Графические функции. Произвольные графики функций. Что такое к в графике функций.
Y f x 1 на рисунке
Y f x 1 на рисунке
Y f x 1 на рисунке. Нуль функции y f x. Как определить нули функции по графику. Функция y=f x нули функции. Нули функции на графике функции.
Нуль функции y f x. Как определить нули функции по графику. Функция y=f x нули функции. Нули функции на графике функции.
Y f x 1 на рисунке. На рисунке изображён график функции y f x и отмечены точки. В какой из этих точек значение производной наименьшее. Наименьшее значение производной. В какой из точек значение производной наименьшее.
На рисунке изображён график функции y f x и отмечены точки. В какой из этих точек значение производной наименьшее. Наименьшее значение производной. В какой из точек значение производной наименьшее.
Y f x 1 на рисунке. На рисунке изображена график дифференциацимой функции. На рисунке изображён график дифференцируемой функции. График дифференцируемой функции. На рисунке изображён график дифференцируемой функции y f x.
На рисунке изображена график дифференциацимой функции. На рисунке изображён график дифференцируемой функции. График дифференцируемой функции. На рисунке изображён график дифференцируемой функции y f x.
Y f x 1 на рисунке
Y f x 1 на рисунке. На рисунке изображен график функции y f x определенной на интервале -1 13. На рисунке изображён график функции на интервале -1 13. Найти промежутки постоянного знака функции по графику. Определите количество целых чисел XI для которых f XI отрицательно.
На рисунке изображен график функции y f x определенной на интервале -1 13. На рисунке изображён график функции на интервале -1 13. Найти промежутки постоянного знака функции по графику. Определите количество целых чисел XI для которых f XI отрицательно.
Y f x 1 на рисунке. Функция определена на отрезке. Функция y f x. График функции и её производной. Определите по графику количество промежутков убывания функции.
Функция определена на отрезке. Функция y f x. График функции и её производной. Определите по графику количество промежутков убывания функции.
Y f x 1 на рисунке
Y f x 1 на рисунке. Рисунок производной. На рисунке изображён график функции y f x определённой на интервале -2 12. Производная рисунок. График производной sin(x).
Рисунок производной. На рисунке изображён график функции y f x определённой на интервале -2 12. Производная рисунок. График производной sin(x).
Y f x 1 на рисунке. Произвольные графики функций. Графики функций рисунки. График произвольной функции. Функции рисунок.
Произвольные графики функций. Графики функций рисунки. График произвольной функции. Функции рисунок.
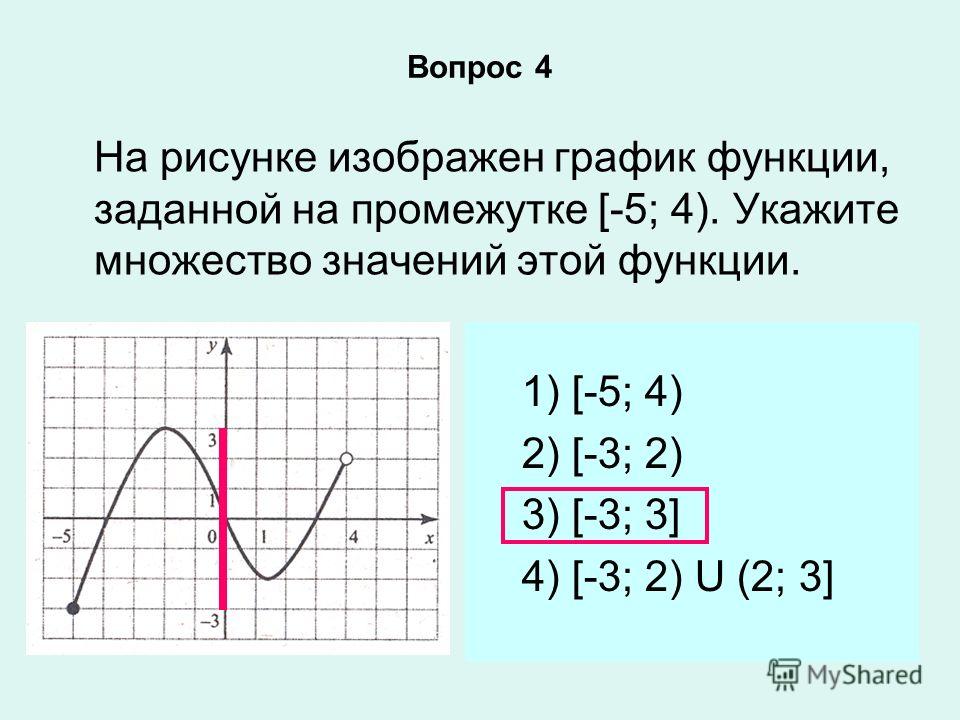
Y f x 1 на рисунке
Y f x 1 на рисунке. Прямая x/y на рисунке изображён график функции. График p=x/y на рисунке изображён. График x2-4. На рисунке изображен график функции y f x п.
Прямая x/y на рисунке изображён график функции. График p=x/y на рисунке изображён. График x2-4. На рисунке изображен график функции y f x п.
Y f x 1 на рисунке. Перечислите свойства функции. Перечислите свойства функции график которой. Перечислите свойства Графика функции. Описать свойства функции по графику.
Перечислите свойства функции. Перечислите свойства функции график которой. Перечислите свойства Графика функции. Описать свойства функции по графику.
Y f x 1 на рисунке. На рисунке изображён график функции y f x определённой на интервале -2 12. На рисунке изображён график функции f x. На рисунке изображен график функции y f x. Касательная к графику функции параллельна прямой.
На рисунке изображён график функции y f x определённой на интервале -2 12. На рисунке изображён график функции f x. На рисунке изображен график функции y f x. Касательная к графику функции параллельна прямой.
Y f x 1 на рисунке. Касательная к графику функции параллельна оси абсцисс. Касательная к графику функции параллельна оси. Точки в которых касательная параллельна оси абсцисс. Точки в которых касательная параллельна оси x.
Касательная к графику функции параллельна оси абсцисс. Касательная к графику функции параллельна оси. Точки в которых касательная параллельна оси абсцисс. Точки в которых касательная параллельна оси x.
Y f x 1 на рисунке. График функции y f x производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции. Функция принимает наименьшее значение.
График функции y f x производной функции f x. На рисунке изображен график производной. На рисунке изображен график производной функции. Функция принимает наименьшее значение.
Y f x 1 на рисунке. Функция задана графиком. Функция задана графиком на промежутке. График функции на отрезке. Убывание функции на графике.
Функция задана графиком. Функция задана графиком на промежутке. График функции на отрезке. Убывание функции на графике.
Y f x 1 на рисунке. График функции на промежутке 5 -5. Функции рисунок. График рисунок. Что такое к в графике функций.
График функции на промежутке 5 -5. Функции рисунок. График рисунок. Что такое к в графике функций.
Y f x 1 на рисунке. Абсцисса точки Графика функции. Абсциссы точек Графика функции при которых f' x 0. Значение Графика функции. Графики функций в точке х.
Абсцисса точки Графика функции. Абсциссы точек Графика функции при которых f’ x 0. Значение Графика функции. Графики функций в точке х.
Y f x 1 на рисунке. ОГЭ 9 класс математика на рисунке изображен график функции y f x. График функции y = 2 + 1/x на рисунке. F2y. График функции y=3/x изображён на рисунке.
ОГЭ 9 класс математика на рисунке изображен график функции y f x. График функции y = 2 + 1/x на рисунке. F2y. График функции y=3/x изображён на рисунке.
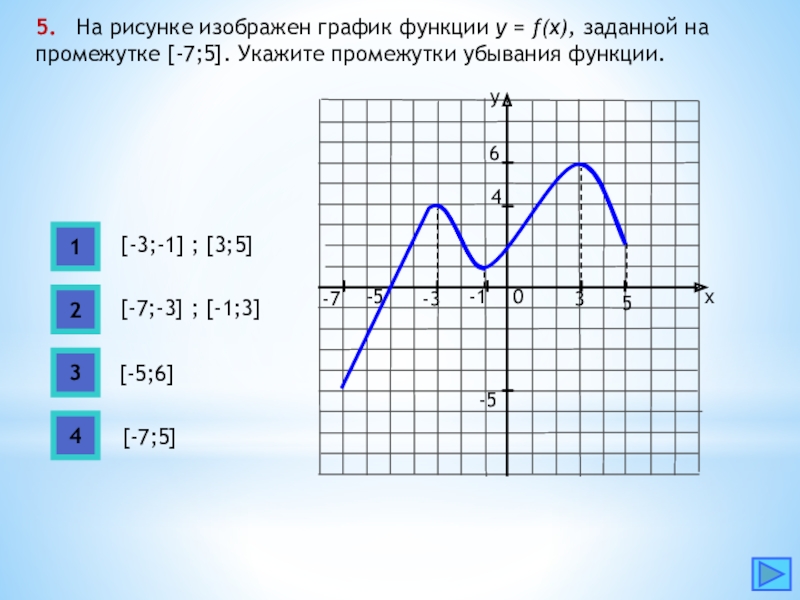
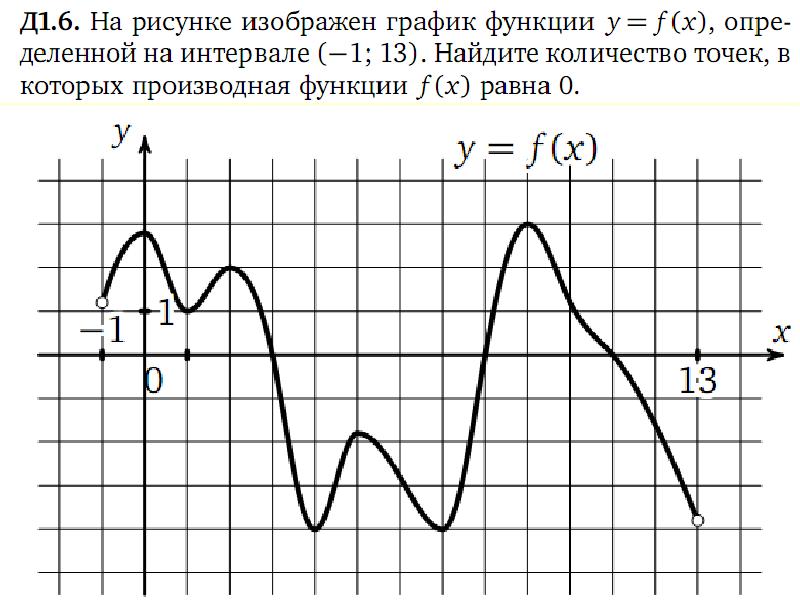
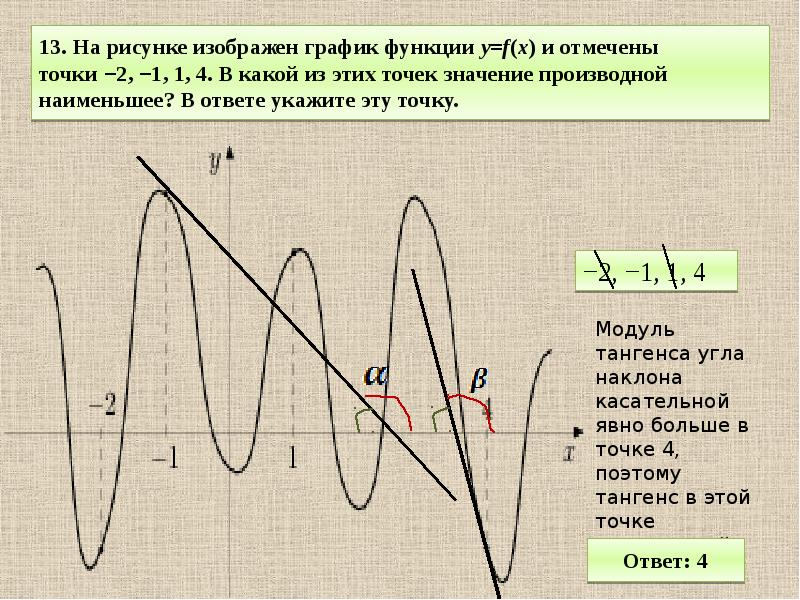
Y f x 1 на рисунке
Y f x 1 на рисунке
Y f x 1 на рисунке. Производная функции f(x) отрицательна. Точки в которых функция отрицательна. Определите количество целых точек, в которых функция отрицательна;. На рисунке изображен график функции определенной на интервале -5 5.
Производная функции f(x) отрицательна. Точки в которых функция отрицательна. Определите количество целых точек, в которых функция отрицательна;. На рисунке изображен график функции определенной на интервале -5 5.
Y f x 1 на рисунке. На рисунке изображен график производной функции f(x) касательная. Касательная к графику функции рисунок. Касательная к графику функции в точке. На рисунке изображен график функции.
На рисунке изображен график производной функции f(x) касательная. Касательная к графику функции рисунок. Касательная к графику функции в точке. На рисунке изображен график функции.
Y f x 1 на рисунке. Функция y f x определена на промежутке -4 4. Определение свойств функции по графику. Область определения функции график. F X на графике.
Функция y f x определена на промежутке -4 4. Определение свойств функции по графику. Область определения функции график. F X на графике.
Y f x 1 на рисунке. Функция f x определена и непрерывна на промежутке -5 6. Функция определена и непрерывна на отрезке -5. Функция y f x. Функция f(x)>0.
Функция f x определена и непрерывна на промежутке -5 6. Функция определена и непрерывна на отрезке -5. Функция y f x. Функция f(x)>0.
Y f x 1 на рисунке. На рисунке изображен график производной и точки x1 x2 x3. На рисунке изображен график функции f x=2x^2-5x+4. F X отрицательна. На рисунке изображён график функции f x найти среди точек.
На рисунке изображен график производной и точки x1 x2 x3. На рисунке изображен график функции f x=2x^2-5x+4. F X отрицательна. На рисунке изображён график функции f x найти среди точек.
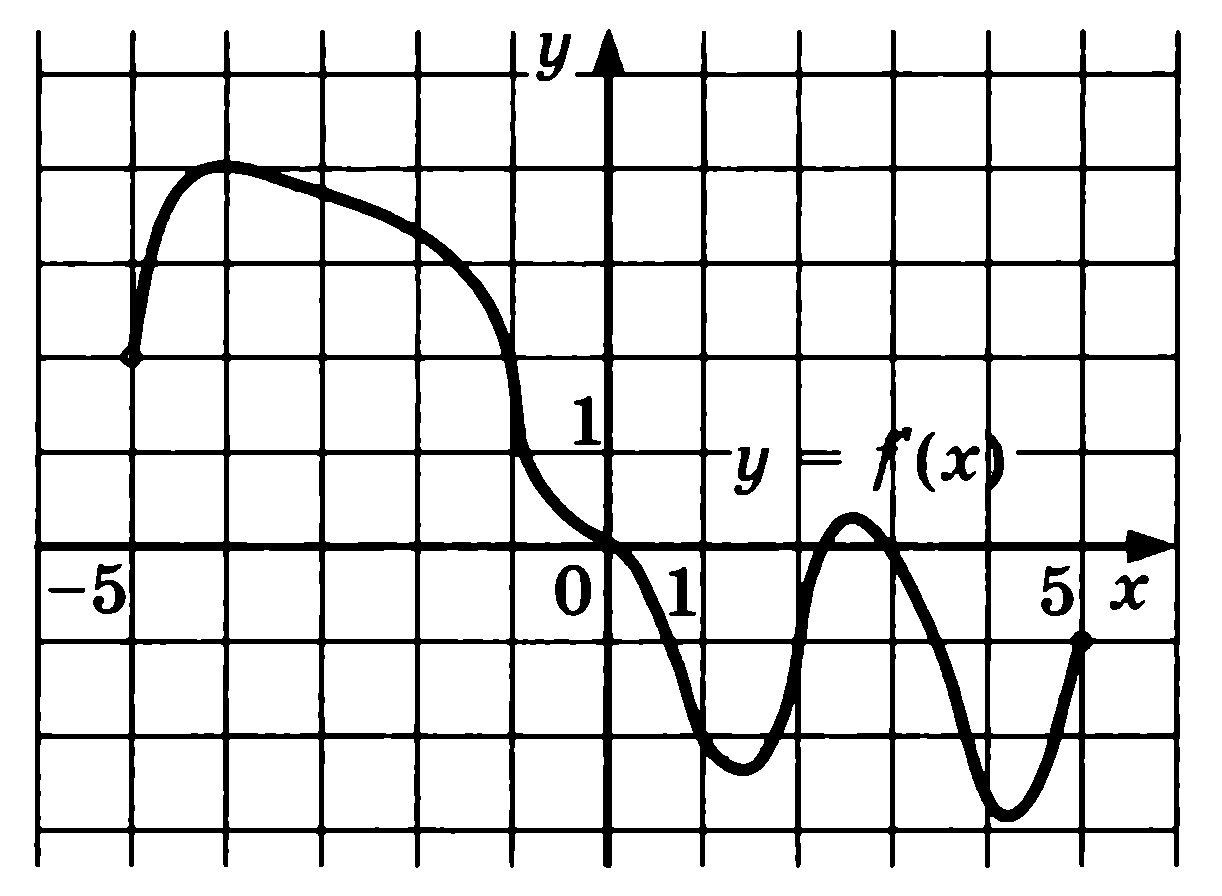
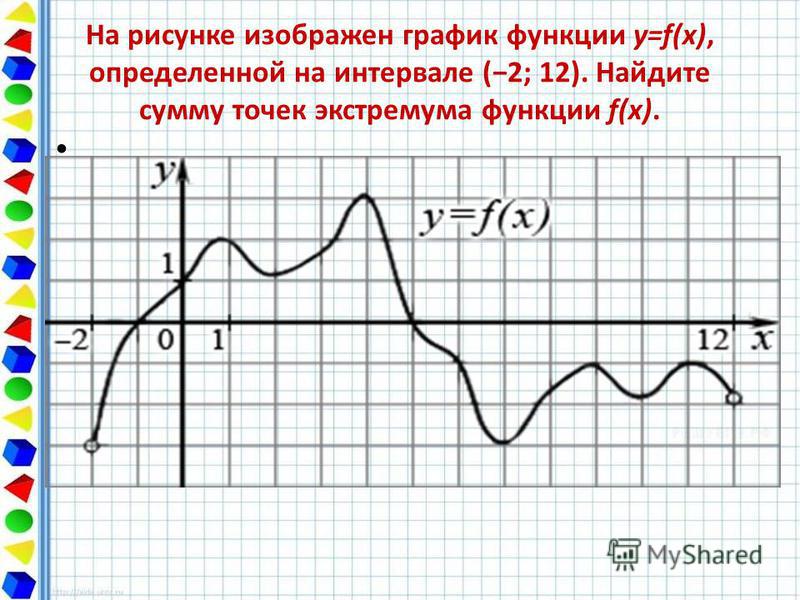
Y f x 1 на рисунке
Y f x 1 на рисунке
Y f x 1 на рисунке. На рисунке изображен график функции заданной на промежутке 5 6. График функции на промежутке. Множество значений функции на промежутке. График функции рисунок.
На рисунке изображен график функции заданной на промежутке 5 6. График функции на промежутке. Множество значений функции на промежутке. График функции рисунок.
Y f x 1 на рисунке. Монотонность функции на графике. Функция убывает на отрезке. Исследуй функцию на монотонность.. График y=f x на отрезке.
Монотонность функции на графике. Функция убывает на отрезке. Исследуй функцию на монотонность.. График y=f x на отрезке.
Y f x 1 на рисунке. График производной f (x)=0. График функции y f x производной функции f x. График производной возрастает если. Как находится производная по графику.
График производной f (x)=0. График функции y f x производной функции f x. График производной возрастает если. Как находится производная по графику.
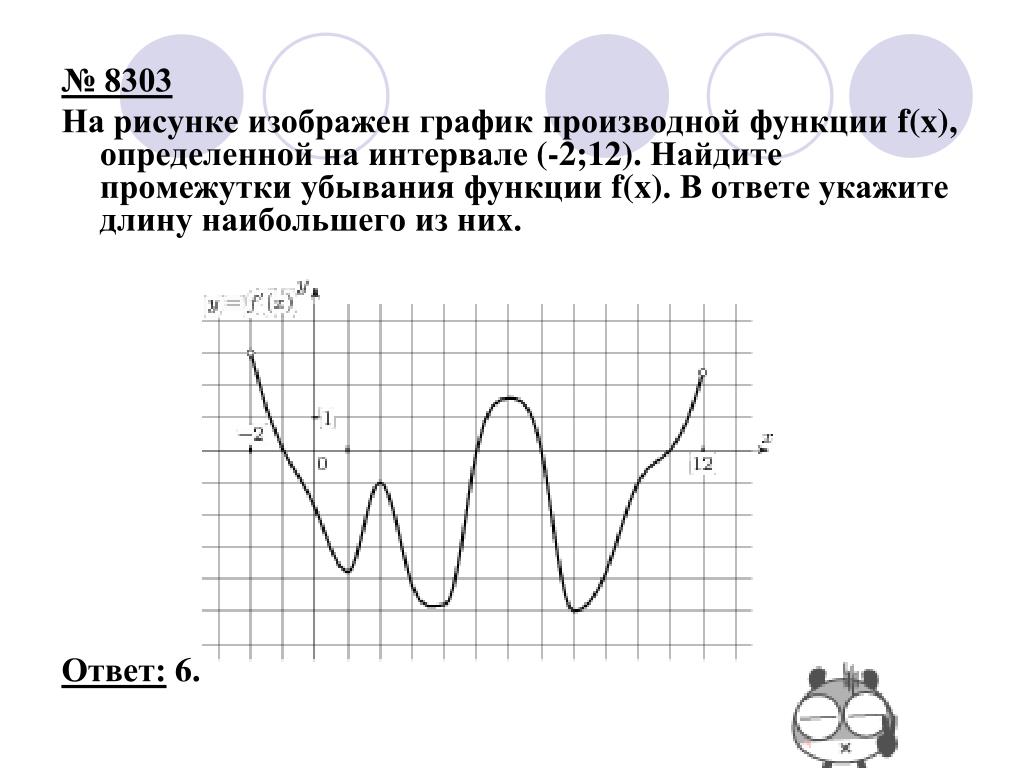
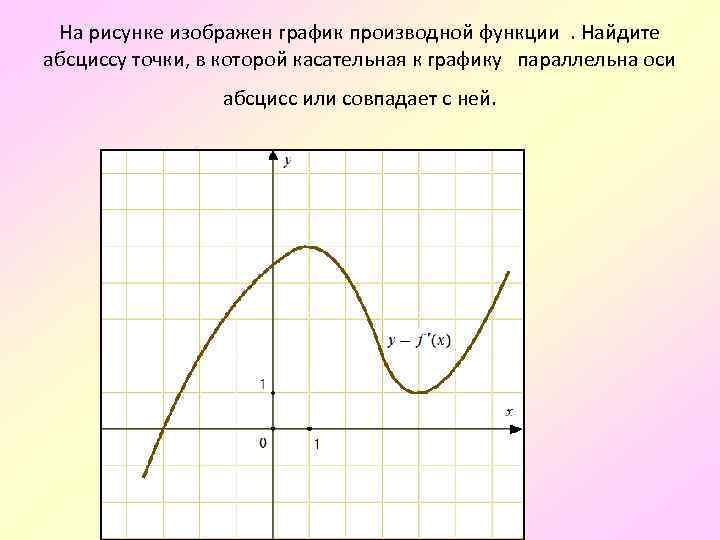
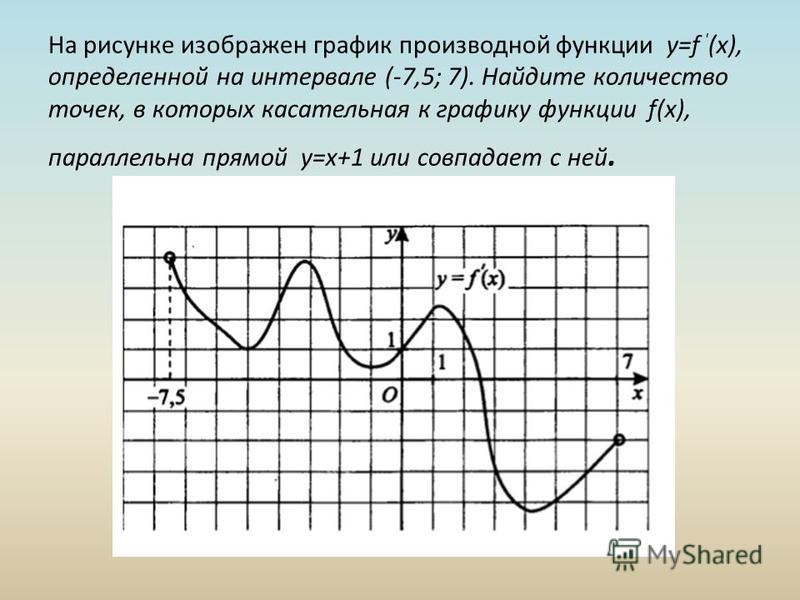
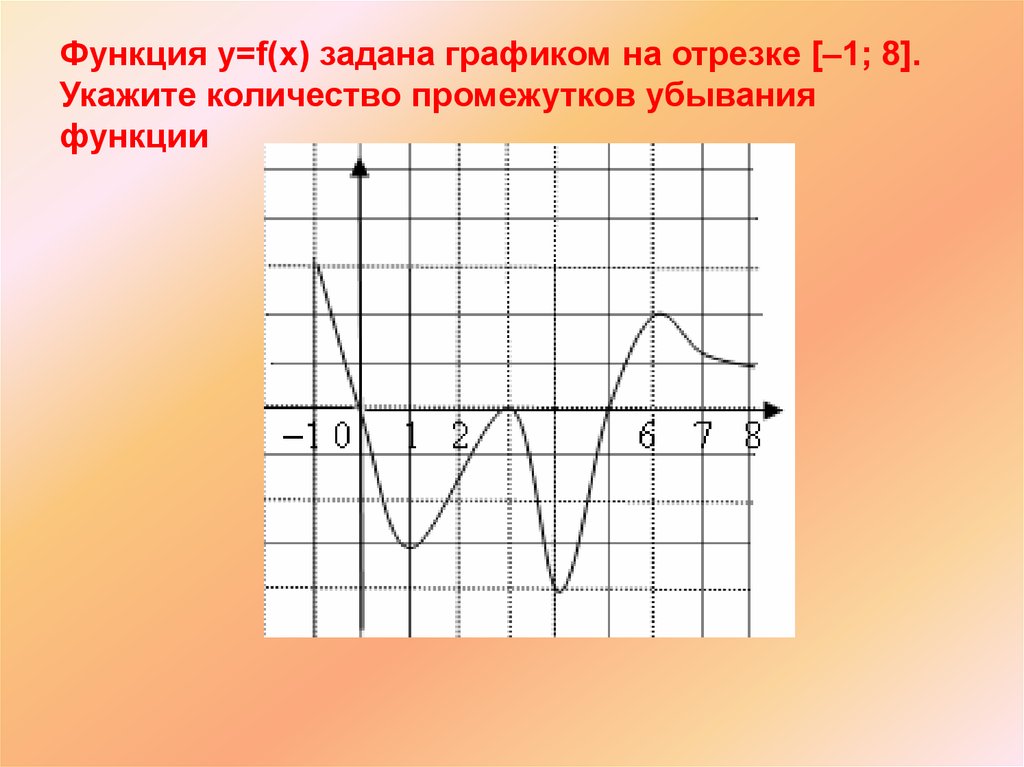
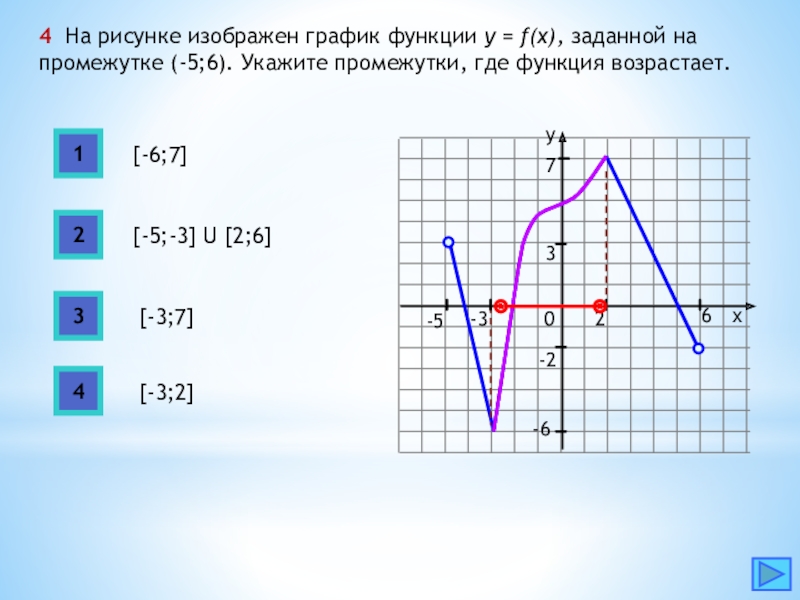
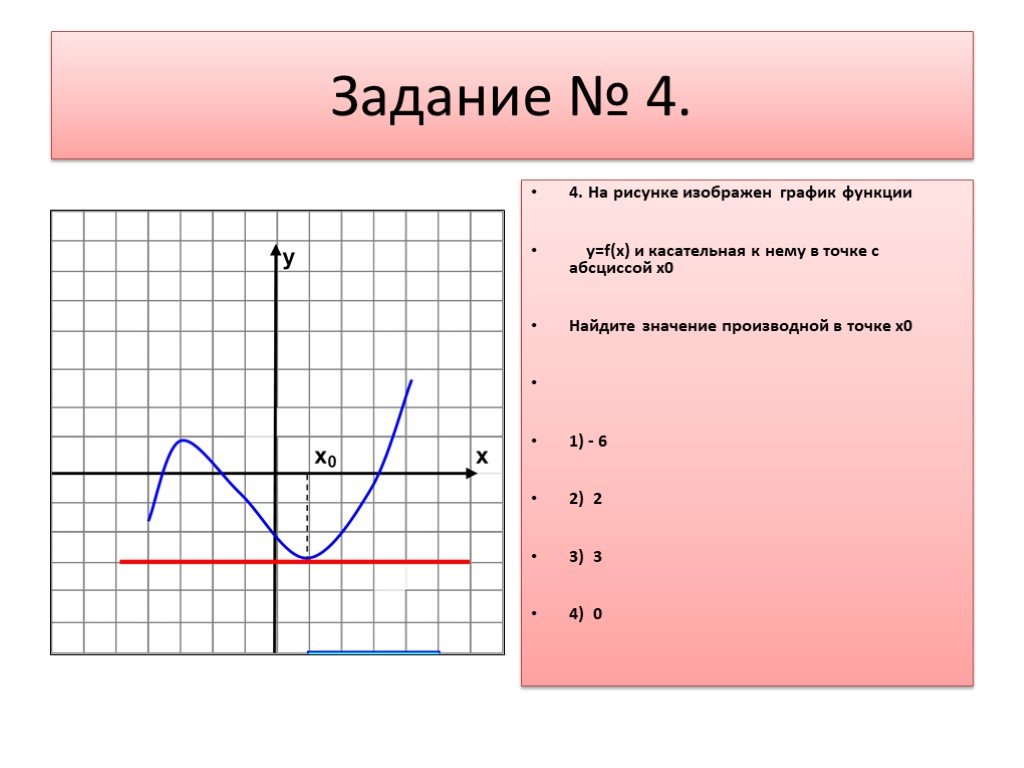
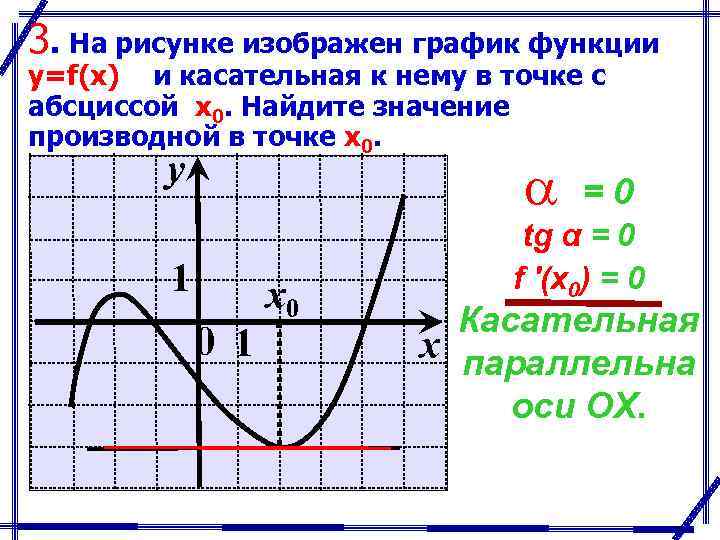
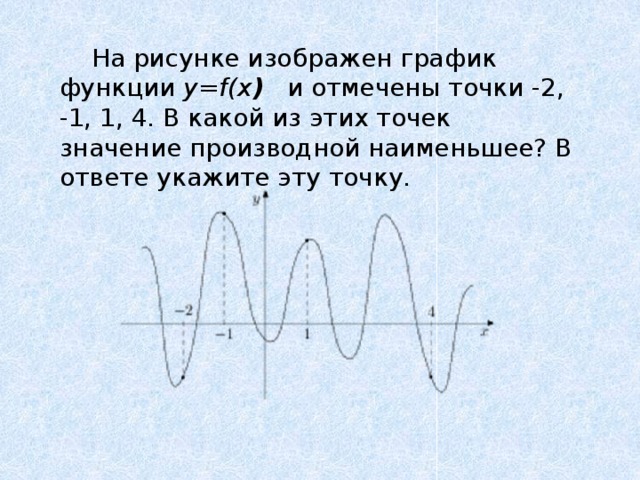
Y f x 1 на рисунке
Y f x 1 на рисунке. Функция возрастает на промежутке [2; +∞). Задание 1. на рисунке изображён график квадратичной функции. Функция возрастает на промежутке (−∞;  −1].. .Изображен график функции y =f(x). какие из утверждений неверны.
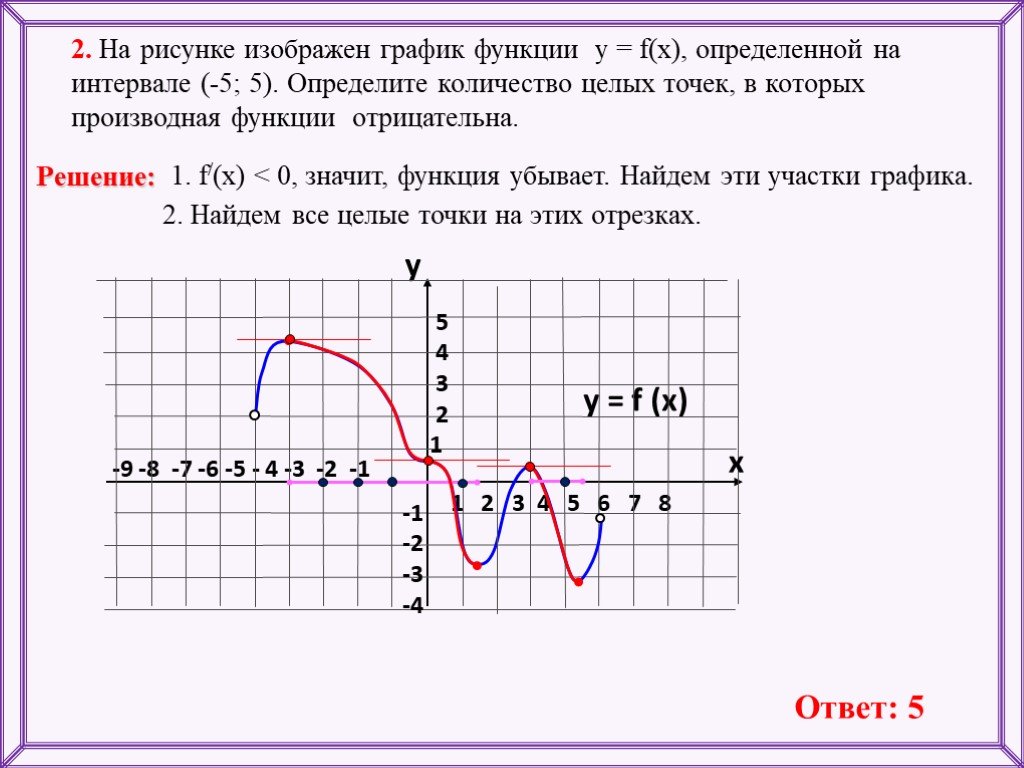
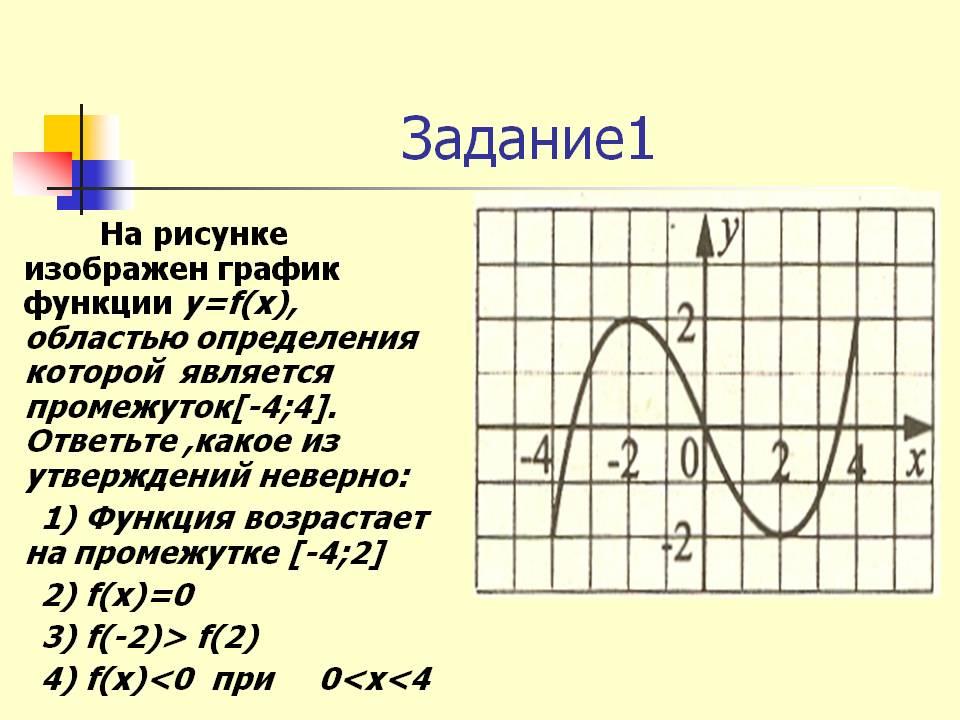
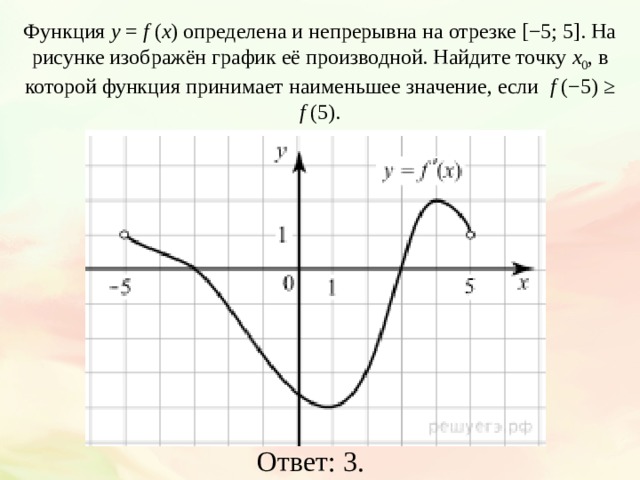
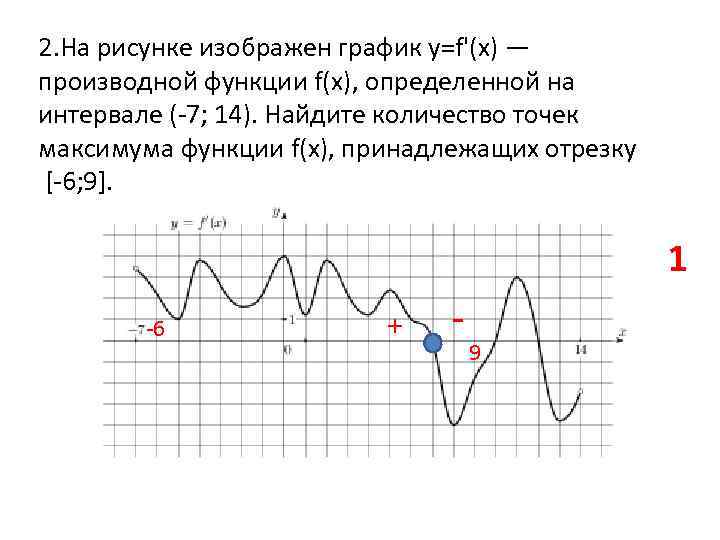
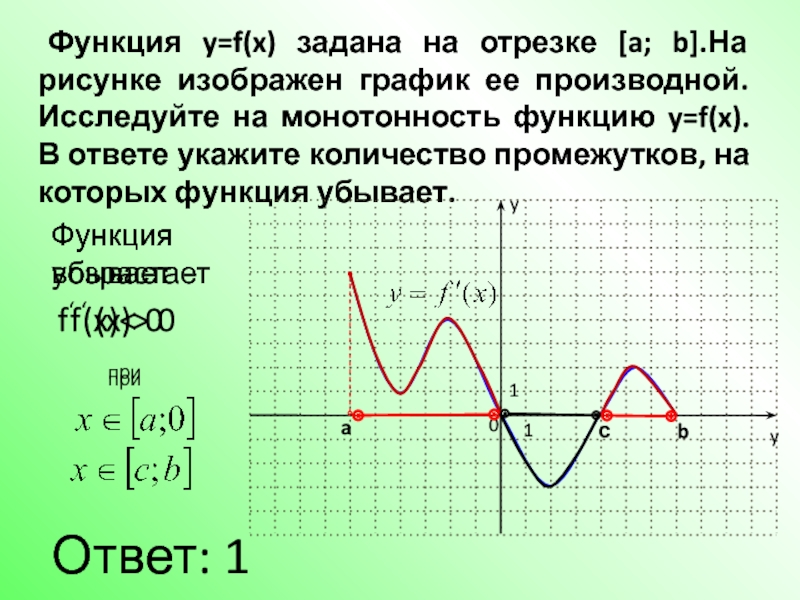
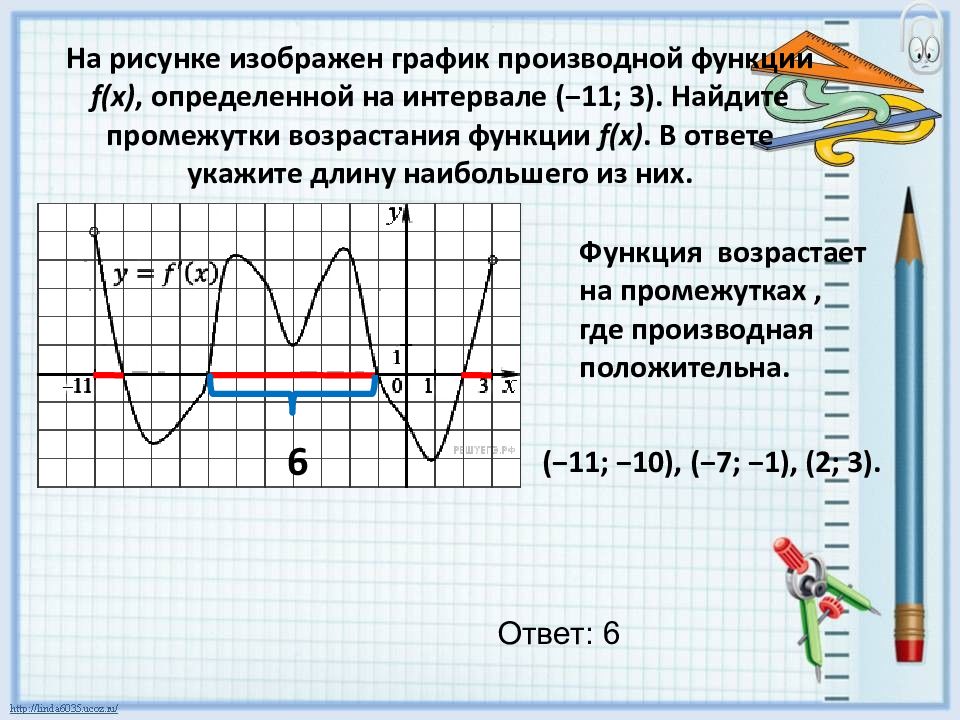
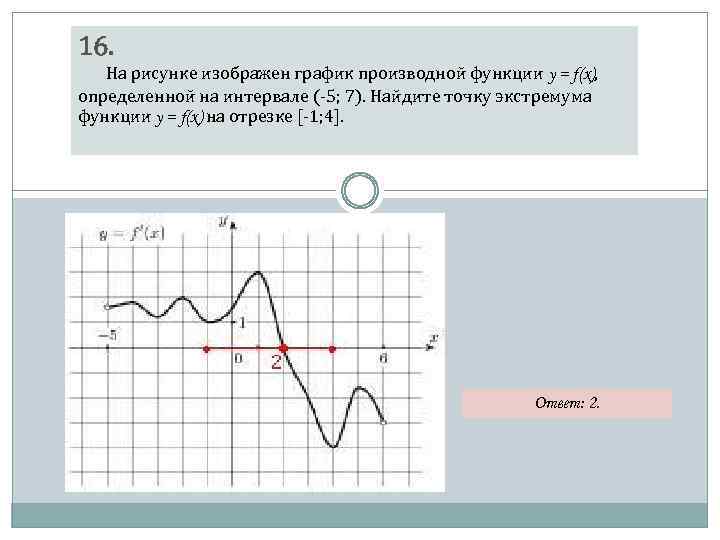
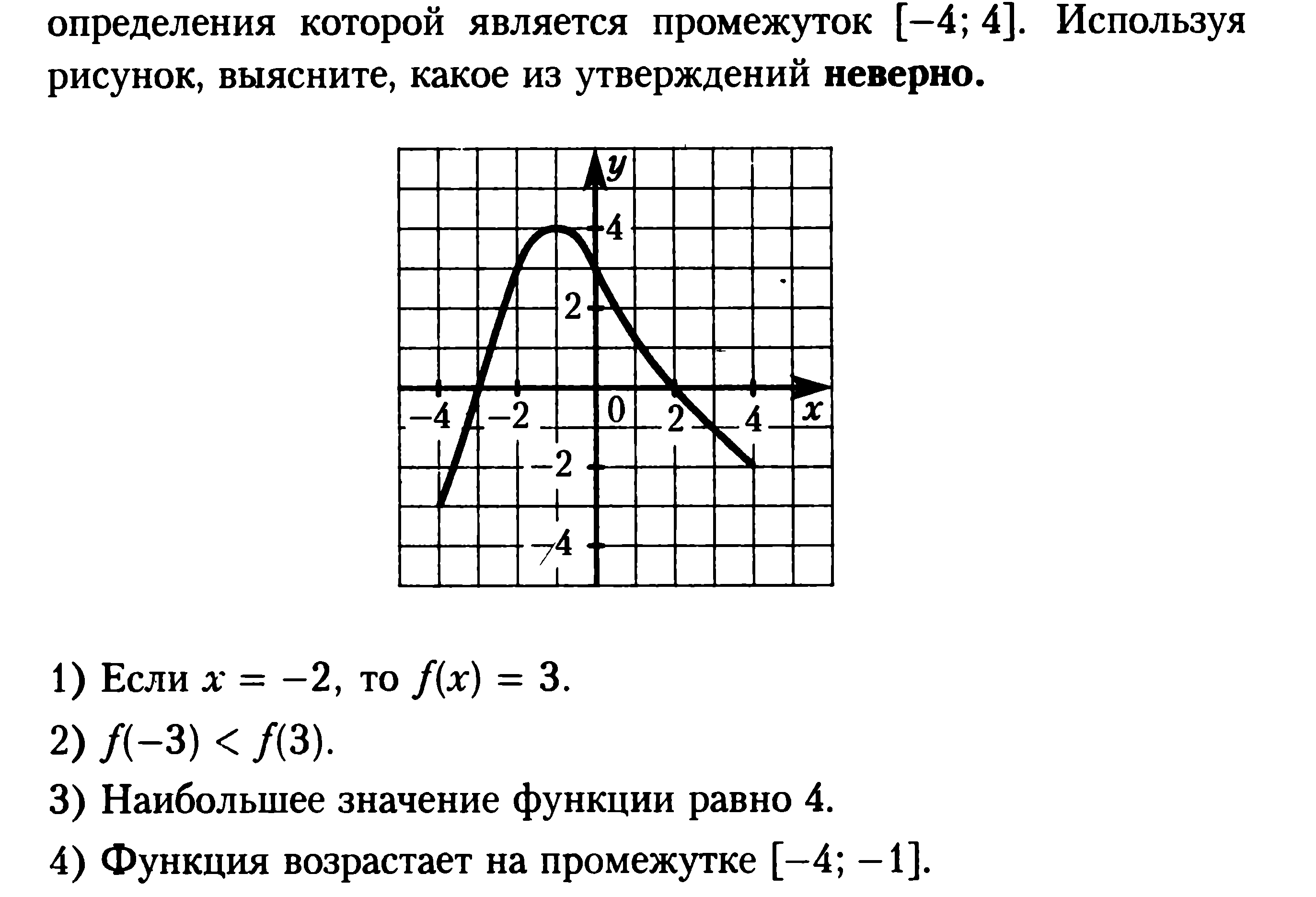
Функция возрастает на промежутке [2; +∞). Задание 1. на рисунке изображён график квадратичной функции. Функция возрастает на промежутке (−∞;  −1].. .Изображен график функции y =f(x). какие из утверждений неверны.
Y f x 1 на рисунке. Картинки нечетных функций. Определите четность функции, изображенной на рисунке.. Определите является ли функция четной или нечетной график. Четная функция картинка.
Картинки нечетных функций. Определите четность функции, изображенной на рисунке.. Определите является ли функция четной или нечетной график. Четная функция картинка.
Y f x 1 на рисунке. Числовая функция рисунок. На рисунке изображен график функции f x a b/x-c. Что такое промежуток на оси Ox рисунок. График функции a b c d.
Числовая функция рисунок. На рисунке изображен график функции f x a b/x-c. Что такое промежуток на оси Ox рисунок. График функции a b c d.
Y f x 1 на рисунке. На рисунке изображен график функции и касательная в точке с абсциссой. Найдите значениефункции в точке ч0. Найти значение производной функции f в точке с абсциссой. Найдите значение производной функции f x.
На рисунке изображен график функции и касательная в точке с абсциссой. Найдите значениефункции в точке ч0. Найти значение производной функции f в точке с абсциссой. Найдите значение производной функции f x.
Y f x 1 на рисунке. ЕГЭ математика профиль максимум и минимум функции.
ЕГЭ математика профиль максимум и минимум функции.
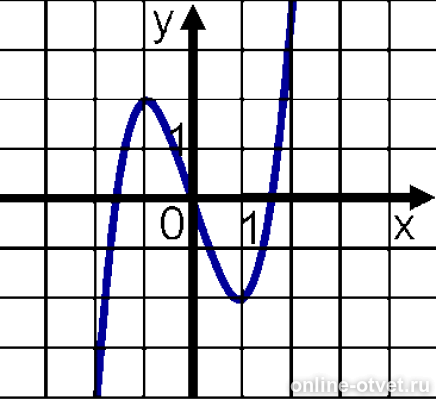
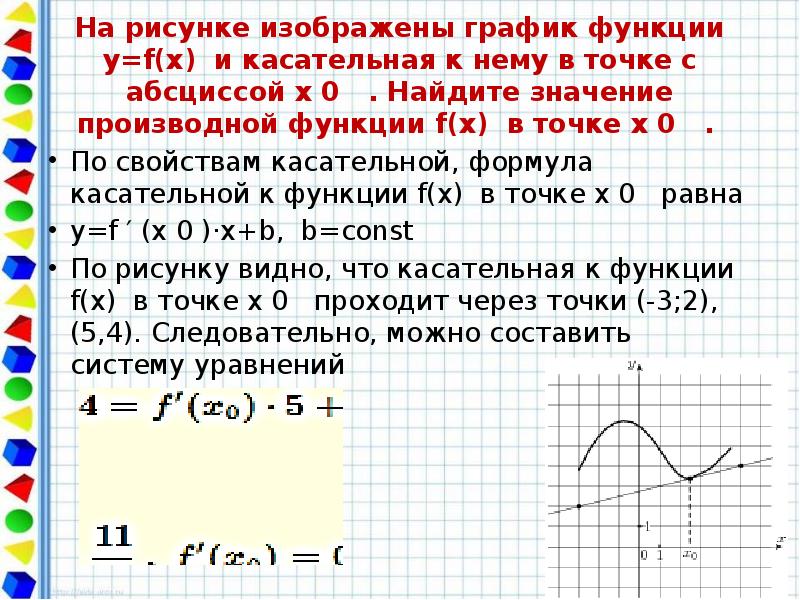
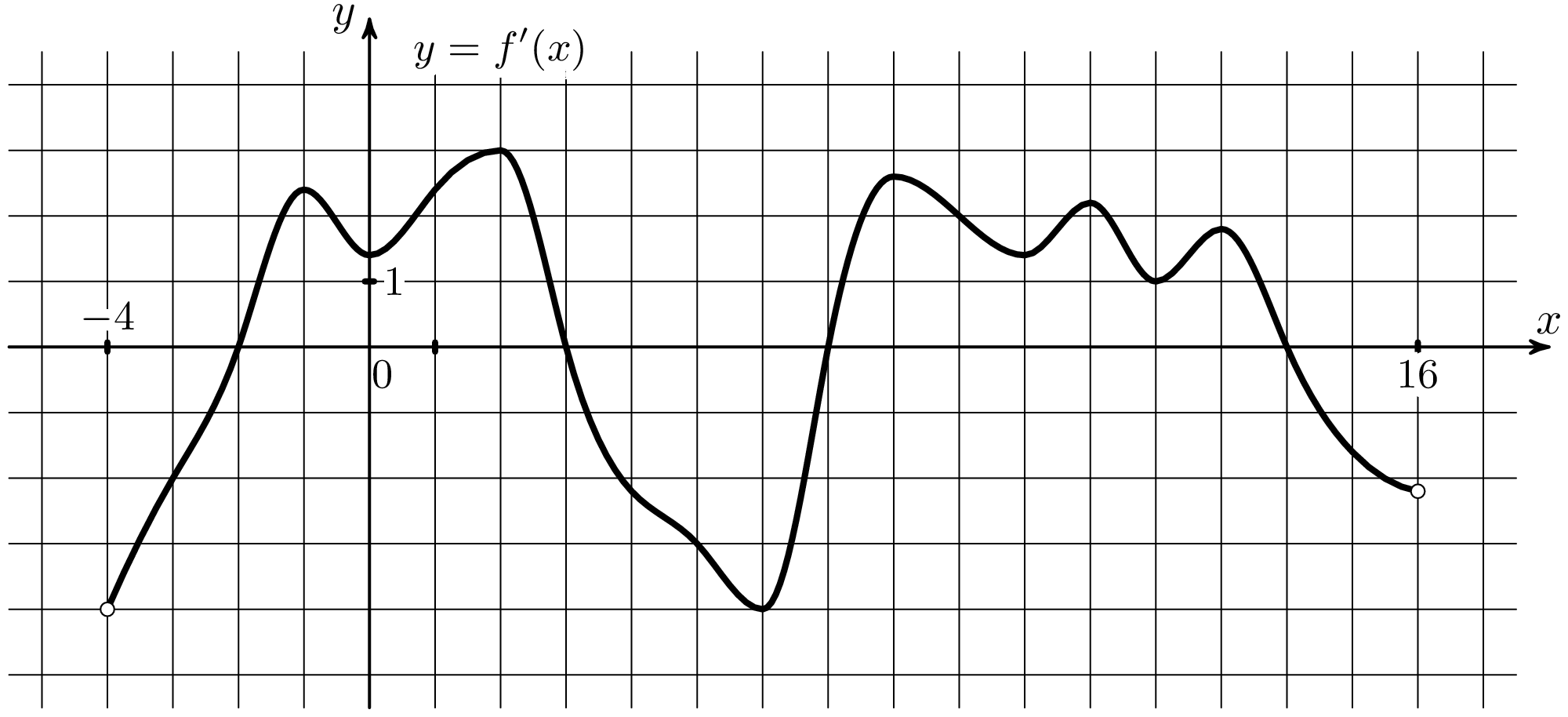
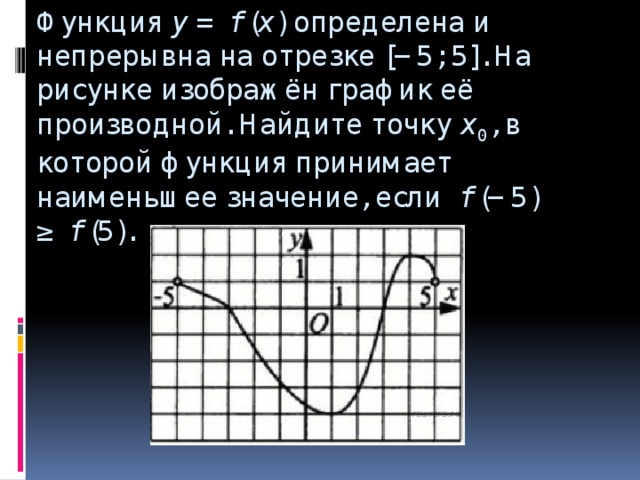
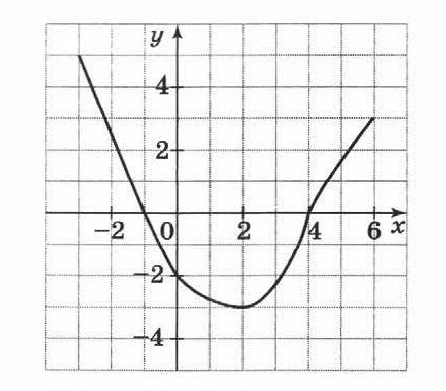
Y f x 1 на рисунке
Y f x 1 на рисунке
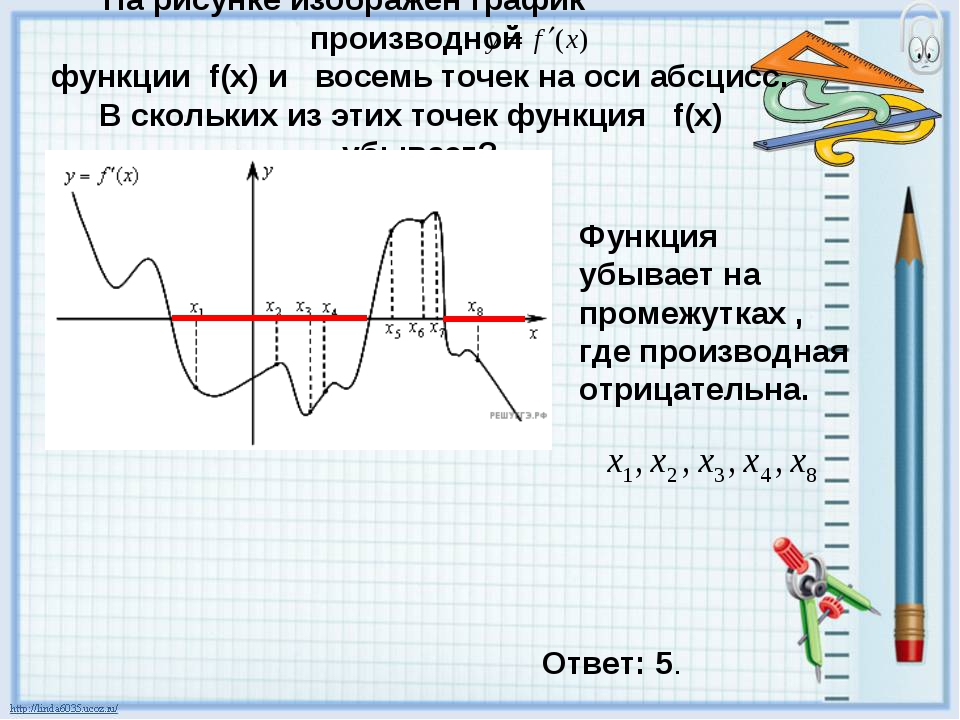
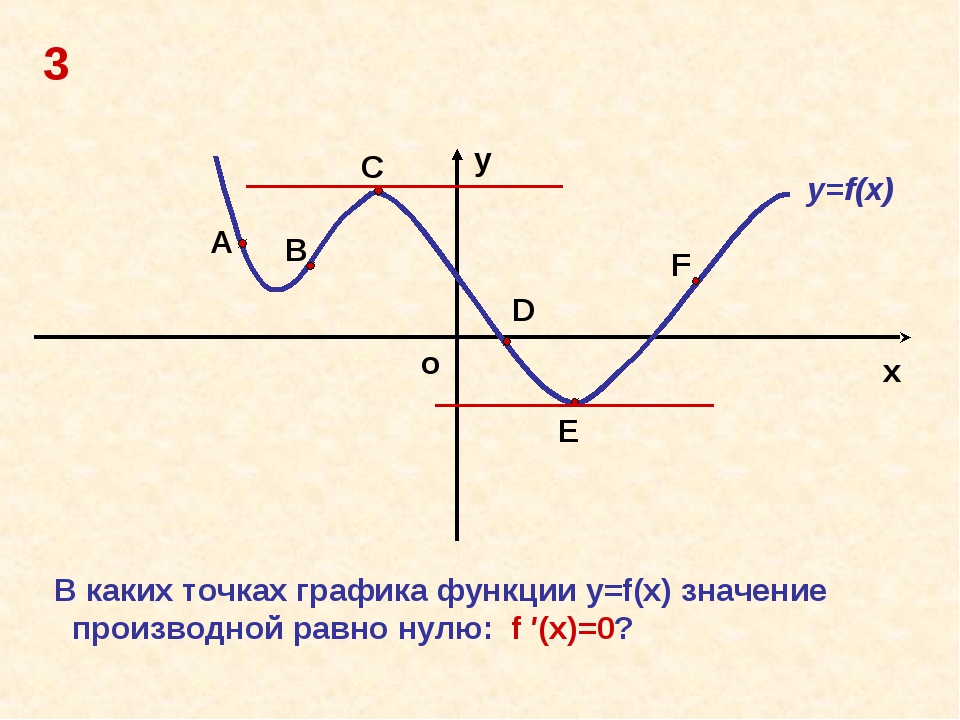
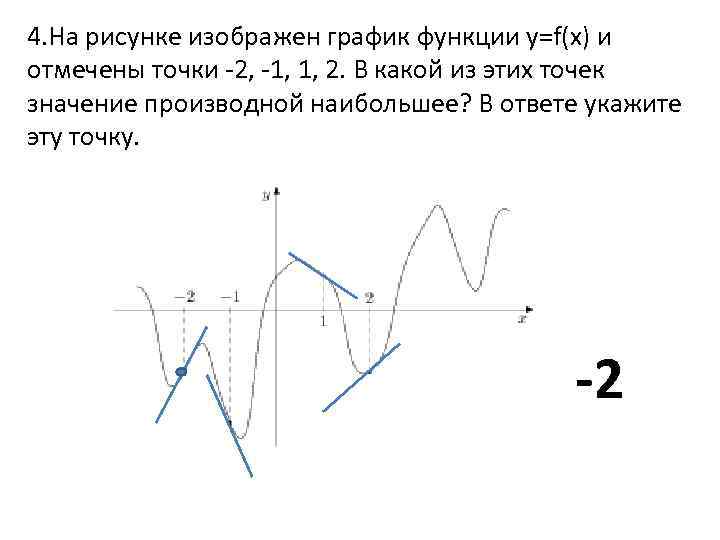
Y f x 1 на рисунке
Y f x 1 на рисунке. График квадратичной функции y = f(x).. Графики ф от х. На рисунках изображены графики квадратичных функций. На рисунке изображен график квадратичной функции.
График квадратичной функции y = f(x).. Графики ф от х. На рисунках изображены графики квадратичных функций. На рисунке изображен график квадратичной функции.
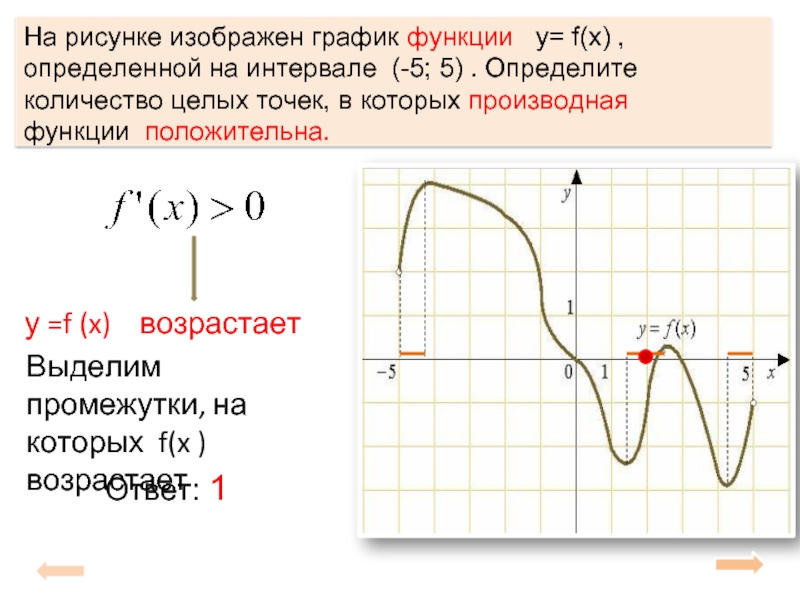
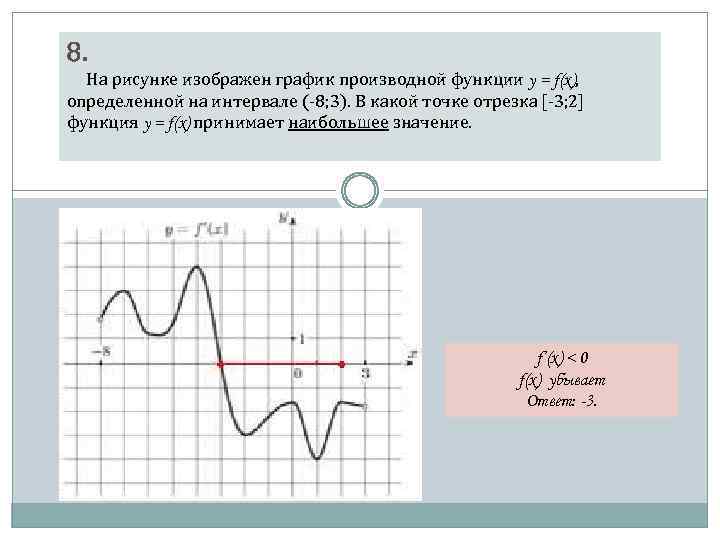
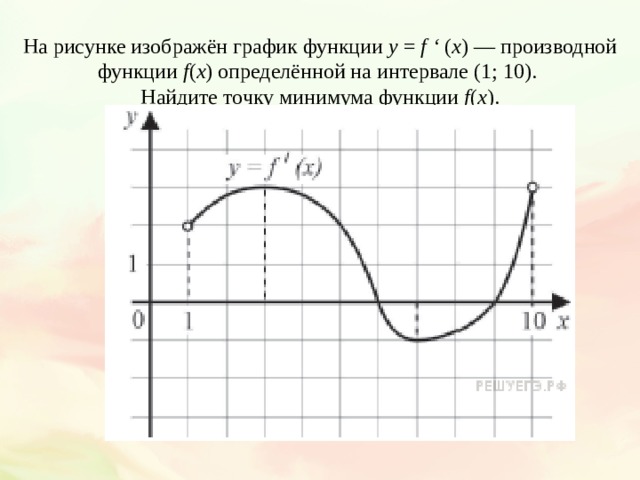
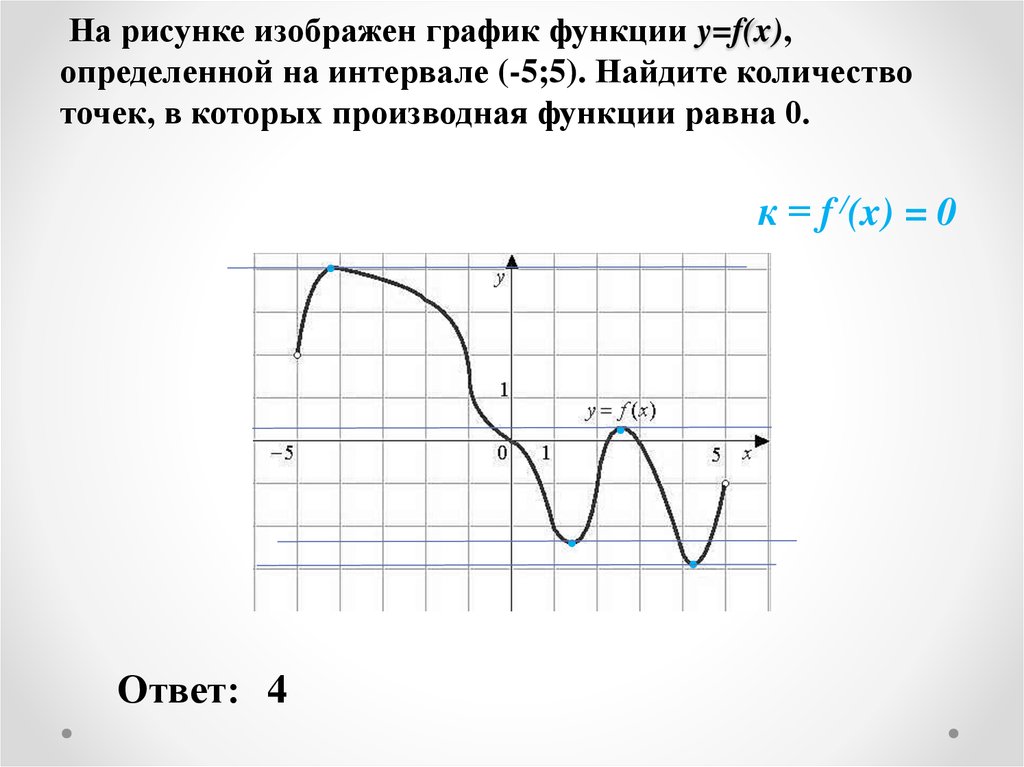
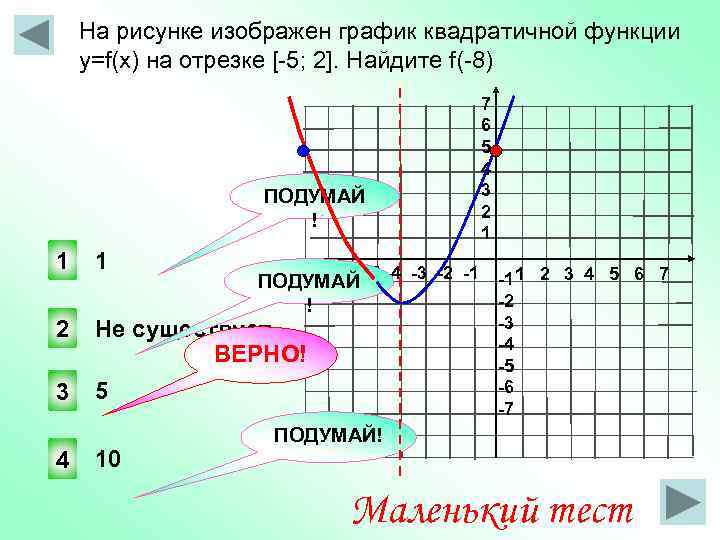
Y f x 1 на рисунке
Y f x 1 на рисунке. График производной функции функция убывает. График производной где функция убывает. Точки производной где функция убывающая. В каких точках производная положительна на графике.
График производной функции функция убывает. График производной где функция убывает. Точки производной где функция убывающая. В каких точках производная положительна на графике.
Y f x 1 на рисунке. Что такое к в графике функций. В каких точках Графика производная равна 0. В каких точках производная функции равна 0. В каких точках производная равна 0 на графике функции.
Что такое к в графике функций. В каких точках Графика производная равна 0. В каких точках производная функции равна 0. В каких точках производная равна 0 на графике функции.
Y f x 1 на рисунке. На рисунке изображен график и отмечены точки. На рисунке изображён график функции y f x и отмечены точки -2 -1 1 4. На рисунке изображен график и отмечены точки -2 -1 1 2. На рисунке изображён график функции f x и отмечены точки -2 -1 1 4.
На рисунке изображен график и отмечены точки. На рисунке изображён график функции y f x и отмечены точки -2 -1 1 4. На рисунке изображен график и отмечены точки -2 -1 1 2. На рисунке изображён график функции f x и отмечены точки -2 -1 1 4.
Y f x 1 на рисунке
Y f x 1 на рисунке. Функция y f x определена на промежутке -4 4. Функция y f x определена на промежутке -4 4 на рисунке изображен. Дана функция y f x график которой изображен на рисунке. Дана функция y f x график которой изображен на рисунке постройте график.
Функция y f x определена на промежутке -4 4. Функция y f x определена на промежутке -4 4 на рисунке изображен. Дана функция y f x график которой изображен на рисунке. Дана функция y f x график которой изображен на рисунке постройте график.
Y f x 1 на рисунке. На рисунке изображен график функции. Точки в которых производная функции положительна. Производная положительна когда функция. Функция положительна на всем интервале.
На рисунке изображен график функции. Точки в которых производная функции положительна. Производная положительна когда функция. Функция положительна на всем интервале.
Y f x 1 на рисунке. Производная функции f(x) положительна?. График функции на промежутке. На рисунке изображен график. Производная функции на интервале.
Производная функции f(x) положительна?. График функции на промежутке. На рисунке изображен график. Производная функции на интервале.
Y f x 1 на рисунке. На рисунке изображен график производной функции f x на интервале -8 3. На рисунке изображен график функции y f x наибольшее значение функции. (На рисунке изображён график функции y=f(x) определите на интервале (-8;5). На рисунке изображён график функции y f x производной функции f x -8 3.
На рисунке изображен график производной функции f x на интервале -8 3. На рисунке изображен график функции y f x наибольшее значение функции. (На рисунке изображён график функции y=f(x) определите на интервале (-8;5). На рисунке изображён график функции y f x производной функции f x -8 3.
Y f x 1 на рисунке. Функция возрастает на промежутке 2 бесконечность. Y F X график 2.5 на рисунке изображен. Рисунок на тему график. График функции y=х-5 на рисунке.
Функция возрастает на промежутке 2 бесконечность. Y F X график 2.5 на рисунке изображен. Рисунок на тему график. График функции y=х-5 на рисунке.
Y f x 1 на рисунке. График квадратичной функции y = f(x).. На рисунке изображён график вида f x ax2+BX+C. На рисунке изображен график функции f x ax2+BX+C F -10. Функция возрастает на промежутке (−∞;  −1]..
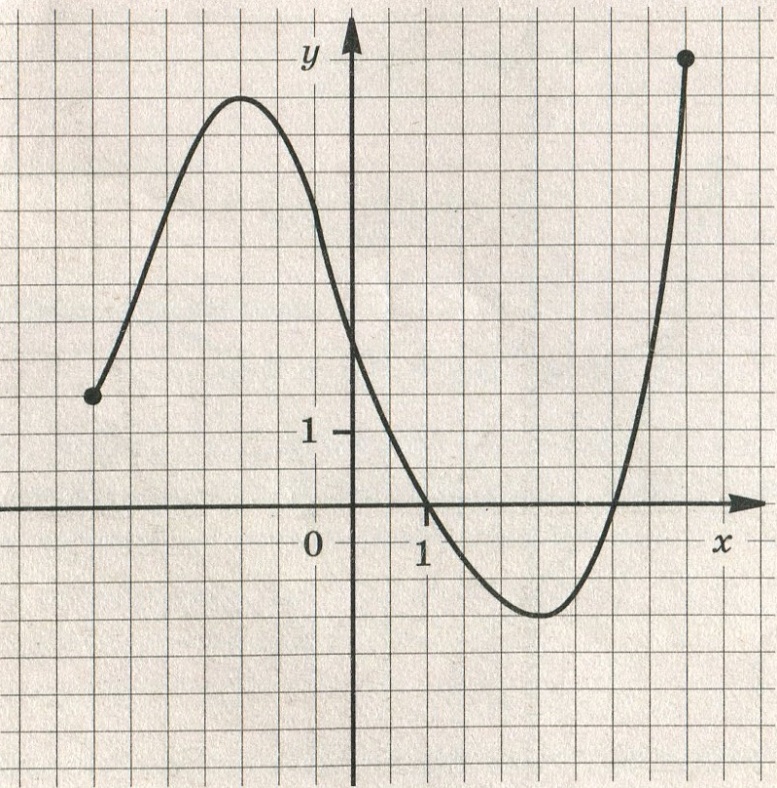
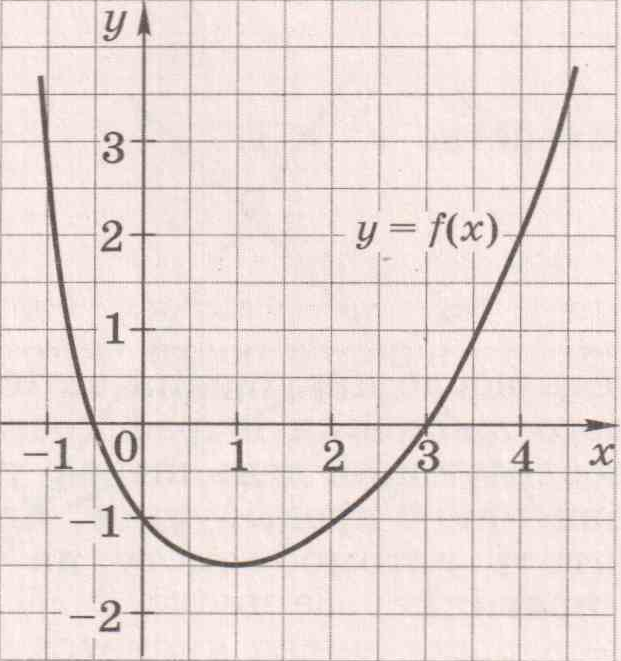
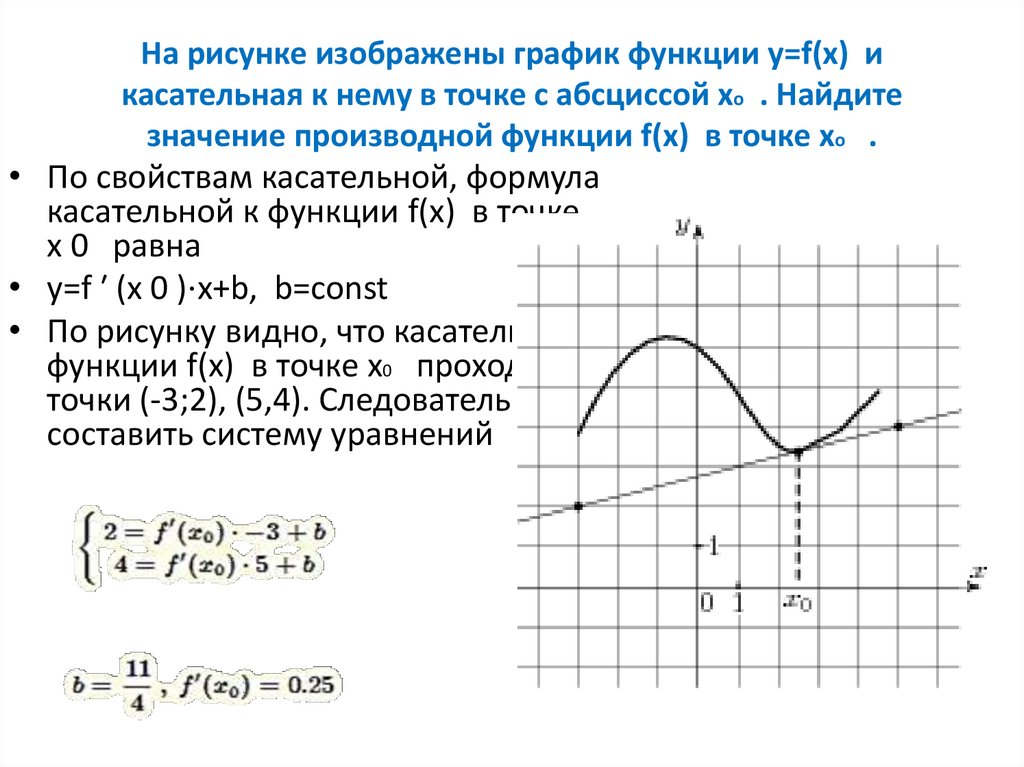
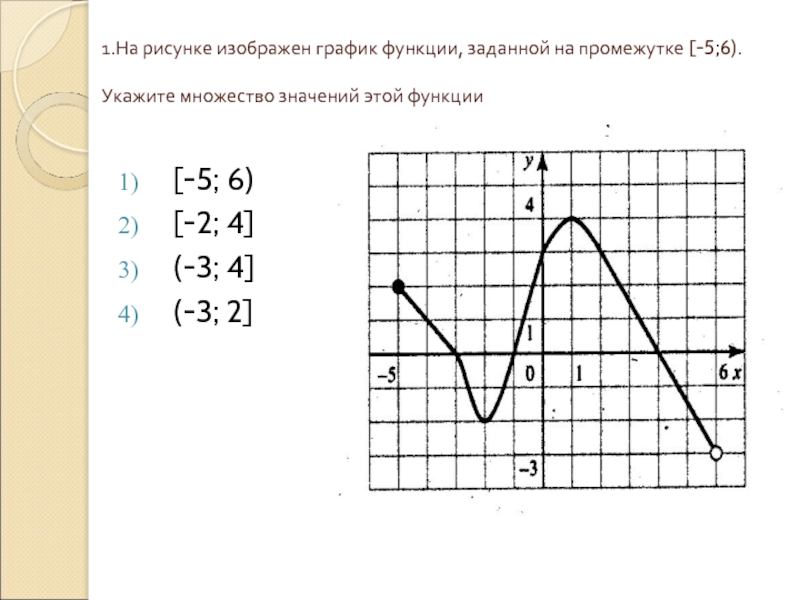
График квадратичной функции y = f(x).. На рисунке изображён график вида f x ax2+BX+C. На рисунке изображен график функции f x ax2+BX+C F -10. Функция возрастает на промежутке (−∞;  −1]..
Y f x 1 на рисунке. Графики четной и нечетной функции примеры. Четные и нечетные функции графики функций. Построить график четной функции. Укажите рисунок на котором изображен график четной функции.
Графики четной и нечетной функции примеры. Четные и нечетные функции графики функций. Построить график четной функции. Укажите рисунок на котором изображен график четной функции.
Y f x 1 на рисунке. На рисунке изображен график производной функции. Промежутки убывания производной функции. График производной промежутки убывания. На рисунке изображен график производной функции f x.
На рисунке изображен график производной функции. Промежутки убывания производной функции. График производной промежутки убывания. На рисунке изображен график производной функции f x.
Y f x 1 на рисунке
Y f x 1 на рисунке. Касательная к графику функции параллельна. Количество точек в которых касательная к графику параллельна. Касателтная к граыику функции параллельная прямой. Найдите количество точек.
Касательная к графику функции параллельна. Количество точек в которых касательная к графику параллельна. Касателтная к граыику функции параллельная прямой. Найдите количество точек.
Y f x 1 на рисунке. В какой из этих точек значение производной наименьшее -2 -1 1 2. График где х а где у.
В какой из этих точек значение производной наименьшее -2 -1 1 2. График где х а где у.
Y f x 1 на рисунке. На рисунке изображён график функции y f x определённой на интервале -7 7. На рисунке 7 изображен график функции y=f(x). На рисунке изображён график функции y f определённой интервале -7 7. На рисунке изображен график -7 7.
На рисунке изображён график функции y f x определённой на интервале -7 7. На рисунке 7 изображен график функции y=f(x). На рисунке изображён график функции y f определённой интервале -7 7. На рисунке изображен график -7 7.
Y f x 1 на рисунке
Y f x 1 на рисунке. Функция определена на промежутке -3 4. Функция y f x определена на промежутке -4 4. Функция у=f(x) отделена на промежутке -3;4. Функция определена на промежутке -3 2.
Функция определена на промежутке -3 4. Функция y f x определена на промежутке -4 4. Функция у=f(x) отделена на промежутке -3;4. Функция определена на промежутке -3 2.
Y f x 1 на рисунке. Область определения функции y=f(x). Область определения функции y f x график. График функции y=f(x)+1. Область определения функции f x.
Область определения функции y=f(x). Область определения функции y f x график. График функции y=f(x)+1. Область определения функции f x.
Y f x 1 на рисунке
Y f x 1 на рисунке. Возрастание и убывание функции производной. Производная возрастает и убывает. Убывающая функция производная. Промежутки убывания функции y f x.
Возрастание и убывание функции производной. Производная возрастает и убывает. Убывающая функция производная. Промежутки убывания функции y f x.
Y f x 1 на рисунке. Y=F(X-A) рисунок. Опишите свойства функции график которой изображен на рисунке. Опишите свойства функции y=f(x). Опишите свойства функции y f x график которой изображен на рисунке.
Y=F(X-A) рисунок. Опишите свойства функции график которой изображен на рисунке. Опишите свойства функции y=f(x). Опишите свойства функции y f x график которой изображен на рисунке.
Y f x 1 на рисунке. Построение графиков функций y f x b и y f x+a. График функции y=f(x). Графики y=f(x). График a^x.
Построение графиков функций y f x b и y f x+a. График функции y=f(x). Графики y=f(x). График a^x.
Y f x 1 на рисунке. На рисунке 9 изображен график функции y=g(x). На рисунке приведен график функции y f x определите длину промежутка. На рисунке 17 изображен график функции y g x. На рисунке 1.41 изображен график.
На рисунке 9 изображен график функции y=g(x). На рисунке приведен график функции y f x определите длину промежутка. На рисунке 17 изображен график функции y g x. На рисунке 1.41 изображен график.
Y f x 1 на рисунке. Касательная к графику производной. Производная в точке по графику. Косательнаяк графику в точке. Касательная к графику функции в точке.
Касательная к графику производной. Производная в точке по графику. Косательнаяк графику в точке. Касательная к графику функции в точке.
Y f x 1 на рисунке. Угловой коэффициент касательной в точке с абсциссой. Определите абсциссы точек в которых угловой коэффициент касательной. К графику функции с абсциссой -3 определите угловой коэффициент.
Угловой коэффициент касательной в точке с абсциссой. Определите абсциссы точек в которых угловой коэффициент касательной. К графику функции с абсциссой -3 определите угловой коэффициент.
Y f x 1 на рисунке. YF hbceyrt BPJ,HF;ty uhfabr aeyrwbb y f(x) b LFYS xbcks s1 s2 s3.
YF hbceyrt BPJ,HF;ty uhfabr aeyrwbb y f(x) b LFYS xbcks s1 s2 s3.
Y f x 1 на рисунке. На рисунке изображен график функции y f x Найдите значение производной. Производная функции FX В точке x0. График функции и касательная с абсциссой x0. График функции и касательная к нему в точке с абсциссой x0.
На рисунке изображен график функции y f x Найдите значение производной. Производная функции FX В точке x0. График функции и касательная с абсциссой x0. График функции и касательная к нему в точке с абсциссой x0.
Y f x 1 на рисунке. Найдите промежутки возрастания функции график производной функции. Возрастание функции на графике производной. График производной промежутки возрастания. Промежутки возрастания функции на графике.
Найдите промежутки возрастания функции график производной функции. Возрастание функции на графике производной. График производной промежутки возрастания. Промежутки возрастания функции на графике.
Y f x 1 на рисунке. Функция y f x определена на промежутке -4 5. На рисунке изображён график функции y f x определённой на промежутке -4 4. Используя график функции y f x определите. На рисунке изображен график функции y f x Найдите f -5.
Функция y f x определена на промежутке -4 5. На рисунке изображён график функции y f x определённой на промежутке -4 4. Используя график функции y f x определите. На рисунке изображен график функции y f x Найдите f -5.
Y f x 1 на рисунке. График функции y 12 x изображен на рисунке.
График функции y 12 x изображен на рисунке.
Y f x 1 на рисунке
Y f x 1 на рисунке. Область определения функции на графике. Область определения функциинамграфике. Функция возрастает на промежутке 1 2. На рисунке изображён график функции y f x Найдите область определения.
Область определения функции на графике. Область определения функциинамграфике. Функция возрастает на промежутке 1 2. На рисунке изображён график функции y f x Найдите область определения.
Y f x 1 на рисунке
Y f x 1 на рисунке
Y f x 1 на рисунке. Касательные к графику функции ЕГЭ. Задачи с касательными к графику. Производные графики функций ЕГЭ. Производная в точке касания по графику.
Касательные к графику функции ЕГЭ. Задачи с касательными к графику. Производные графики функций ЕГЭ. Производная в точке касания по графику.
Y f x 1 на рисунке

Leave a Comment

Your email address will not be published. Required fields are marked *