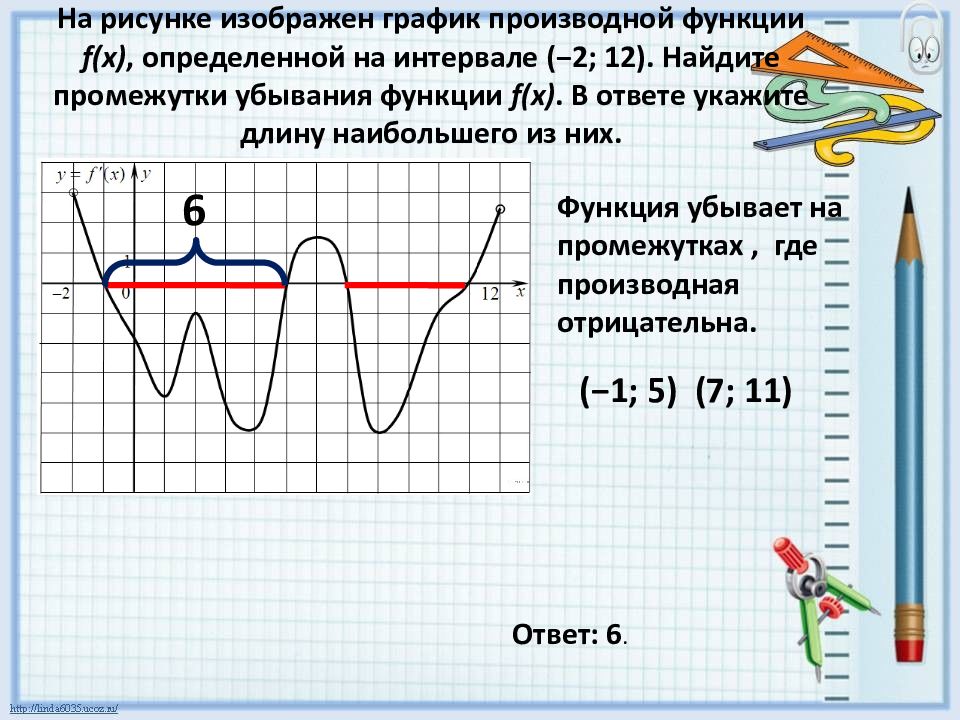
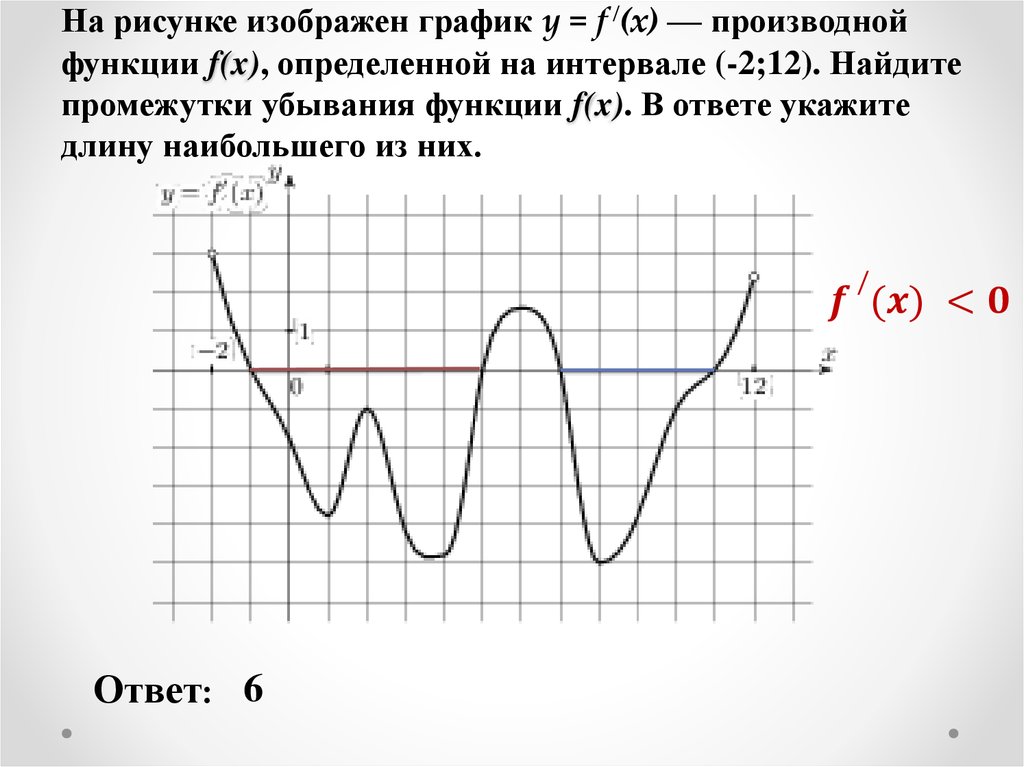
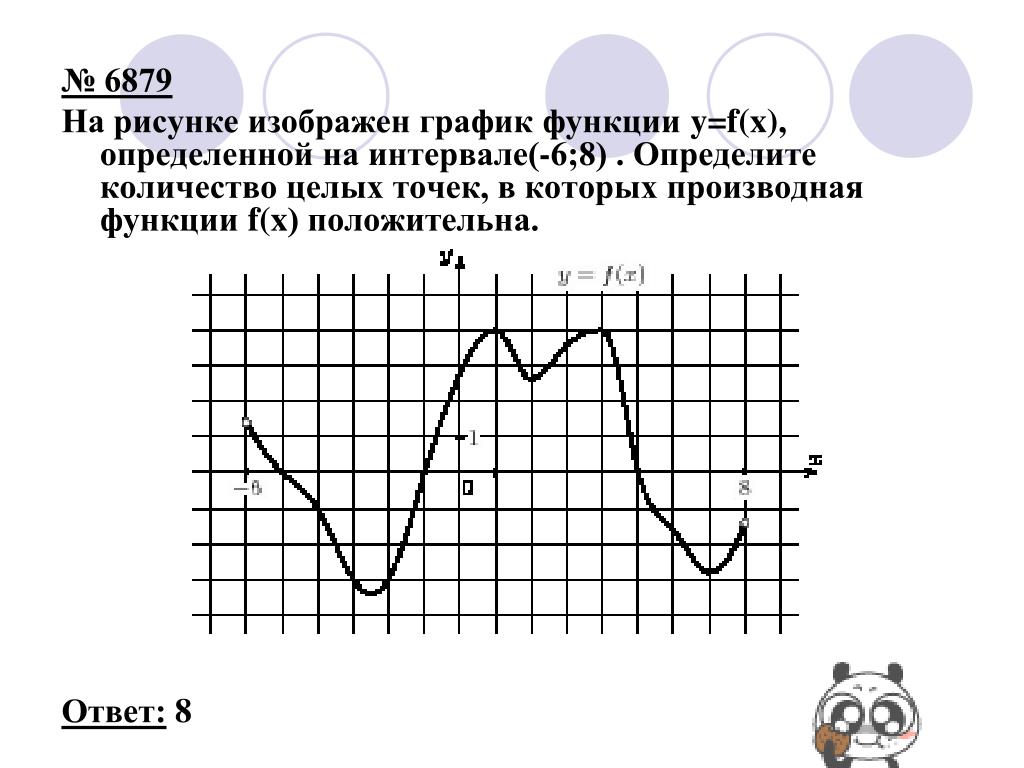
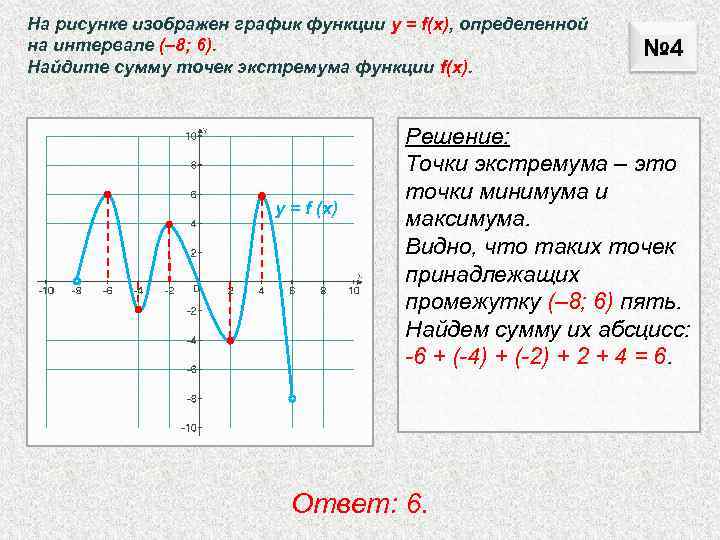
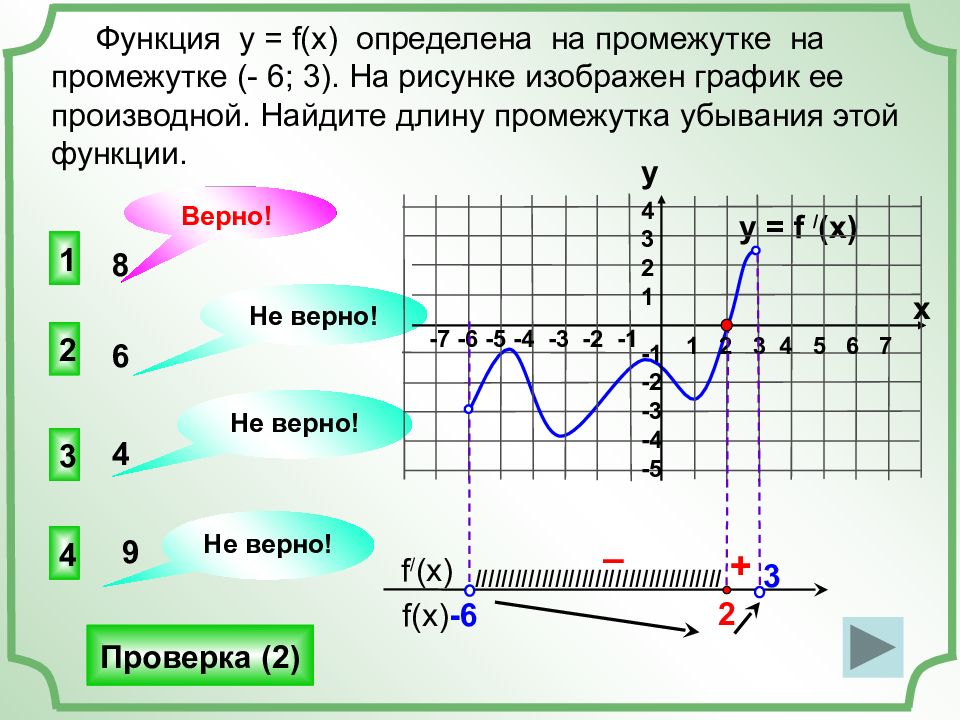
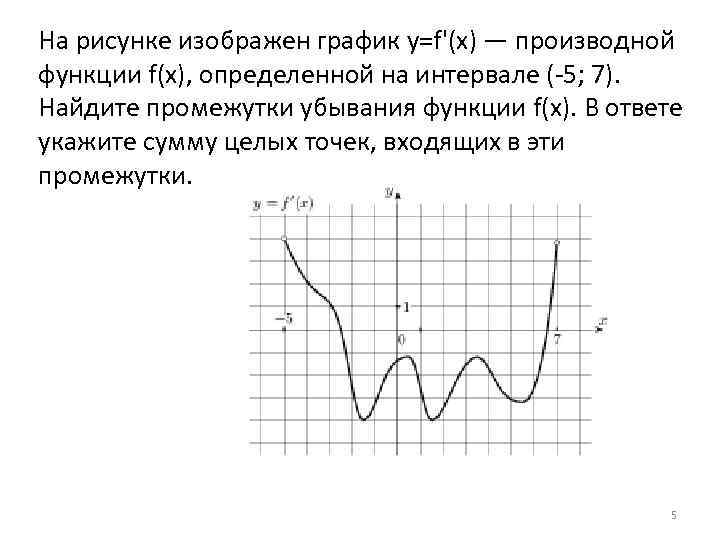
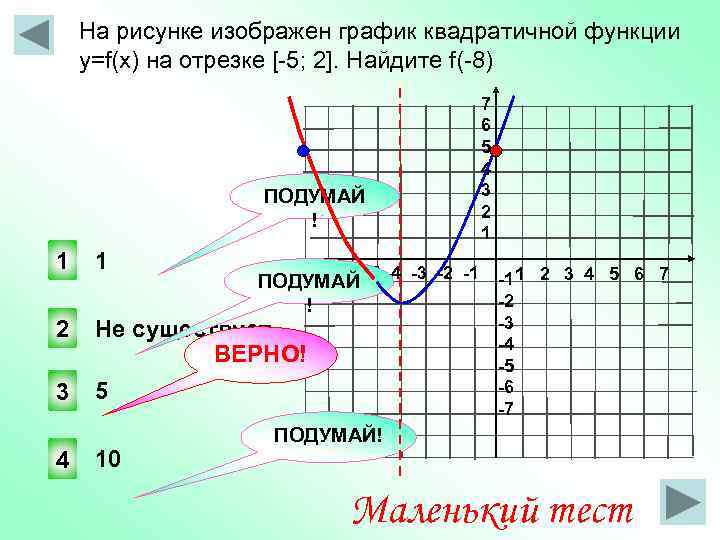
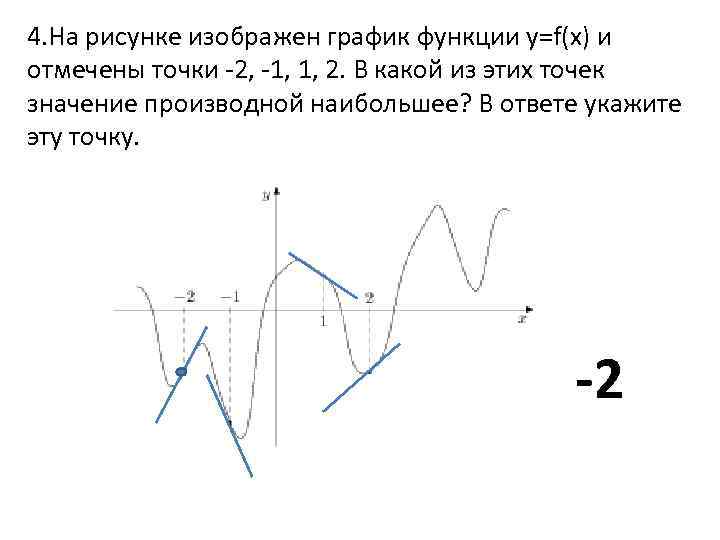
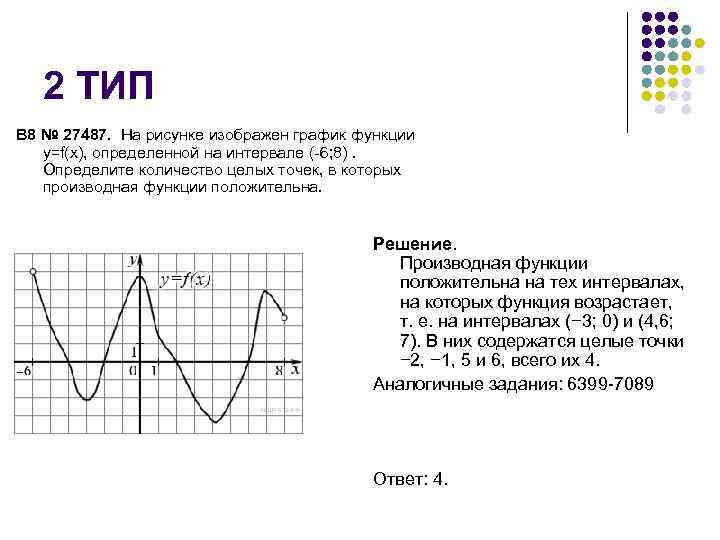
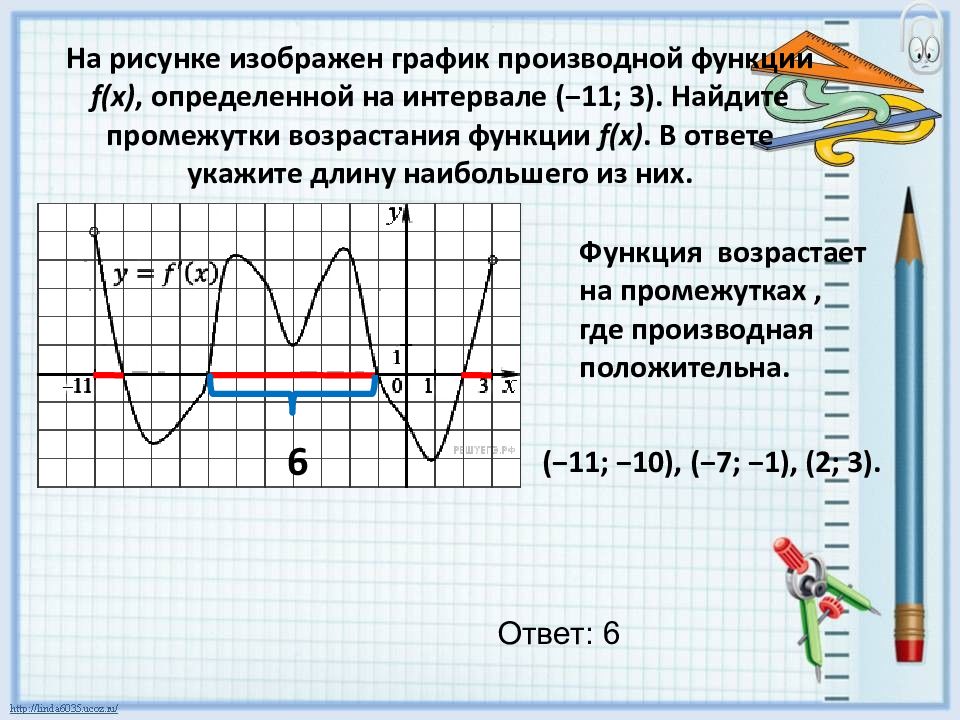
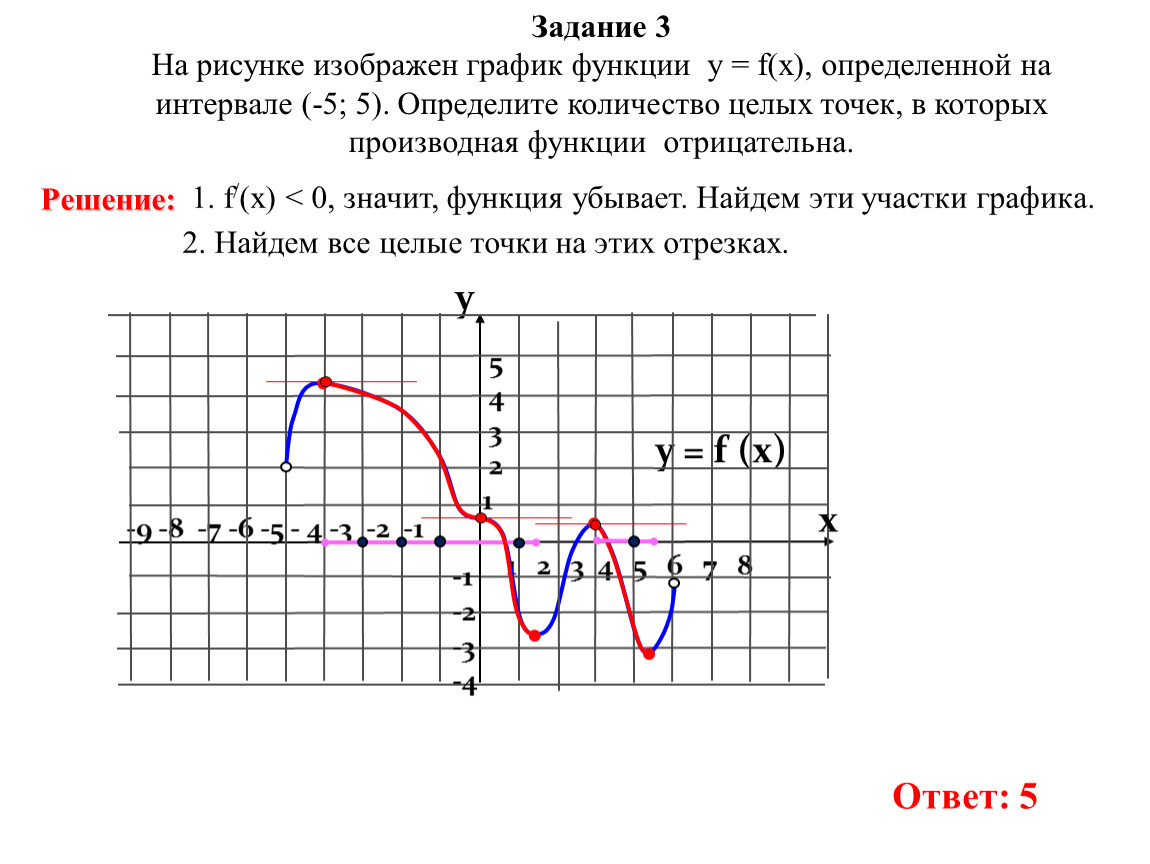
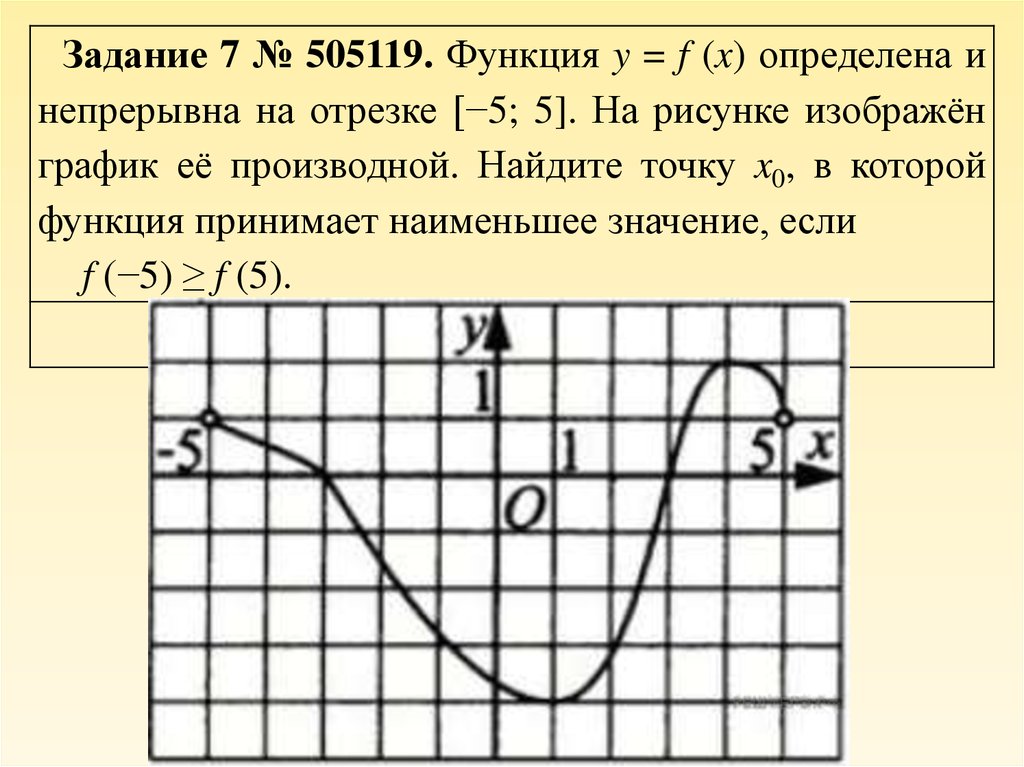
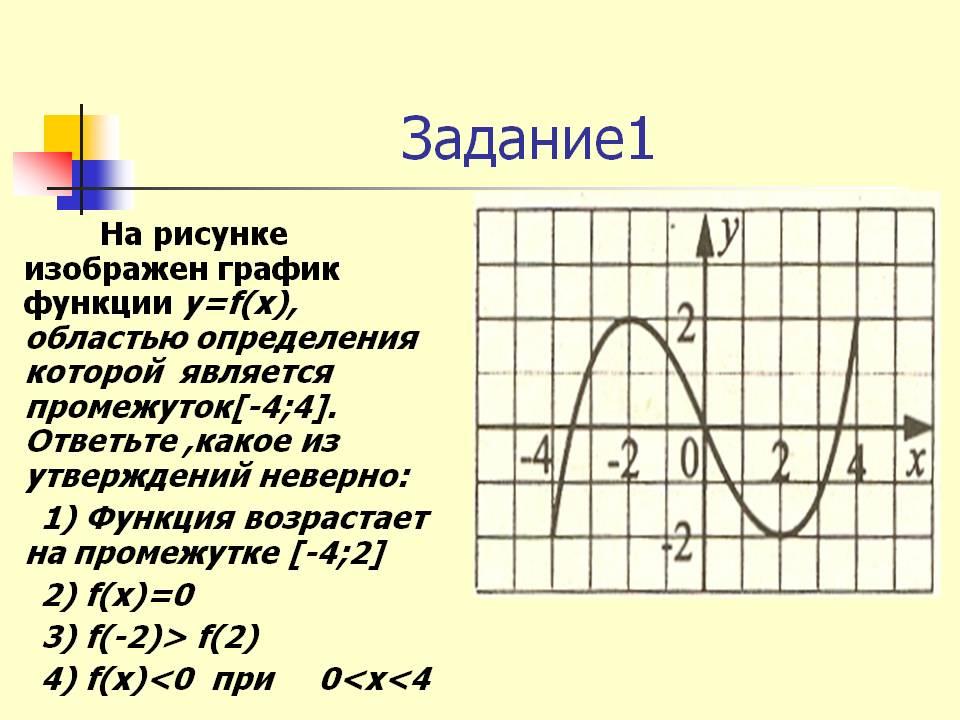
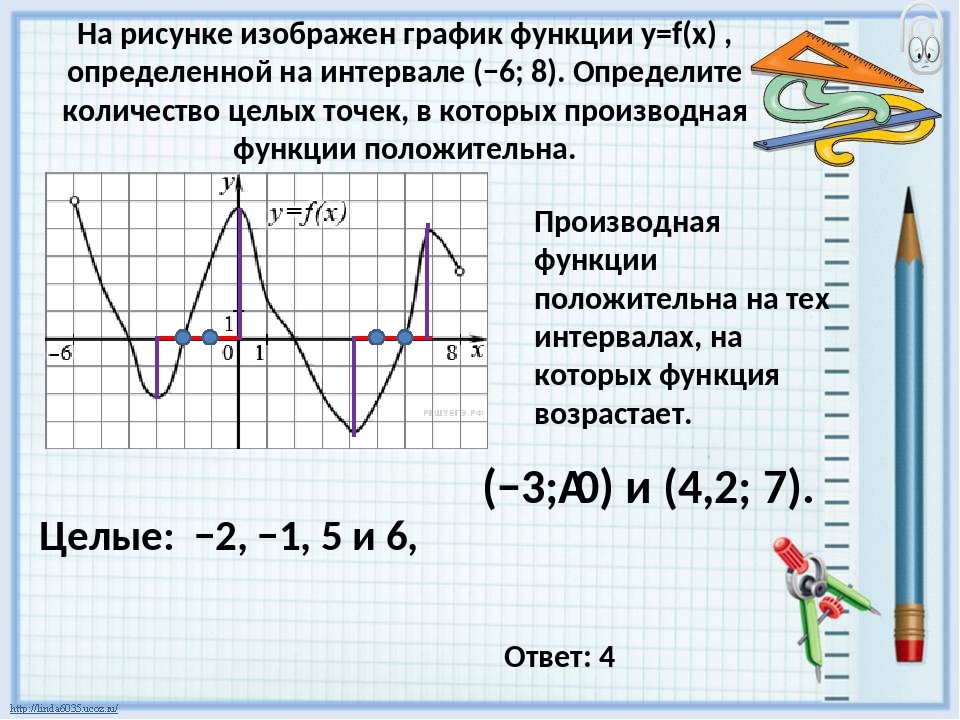
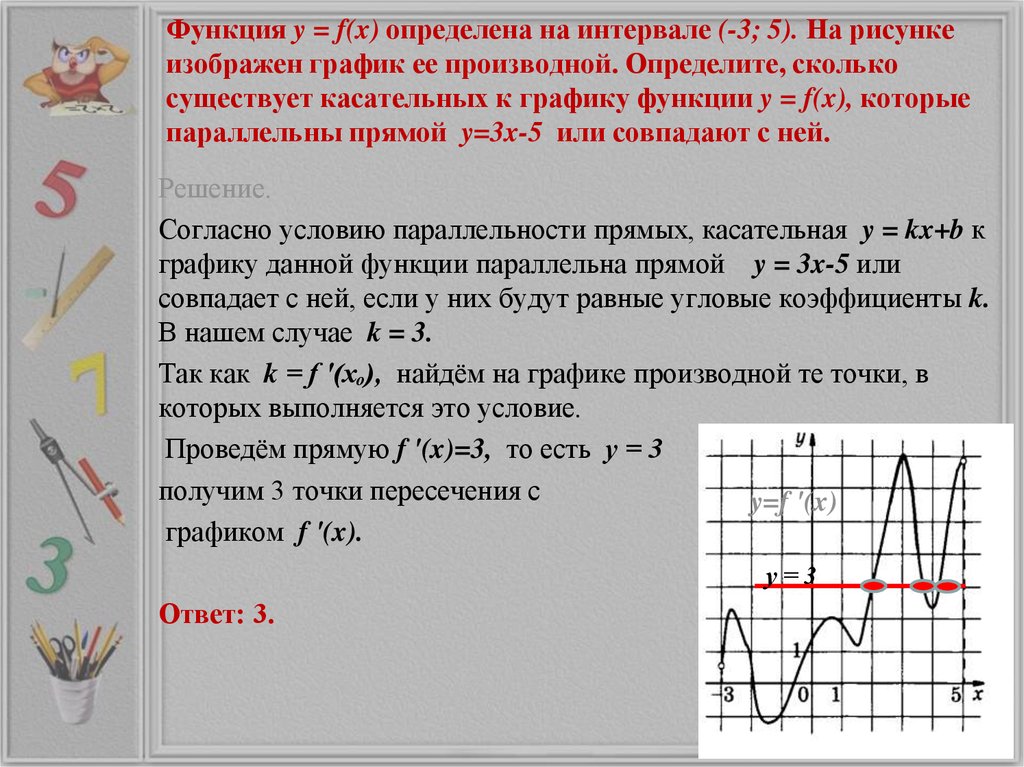
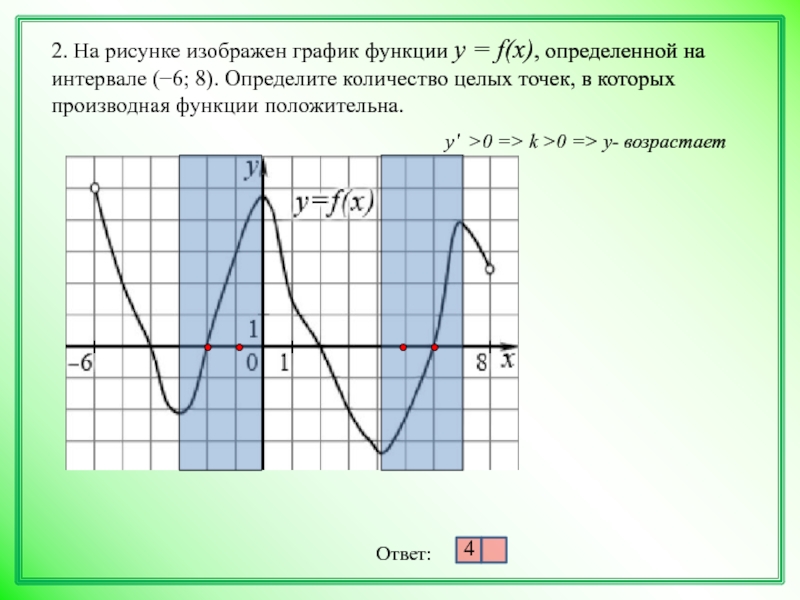
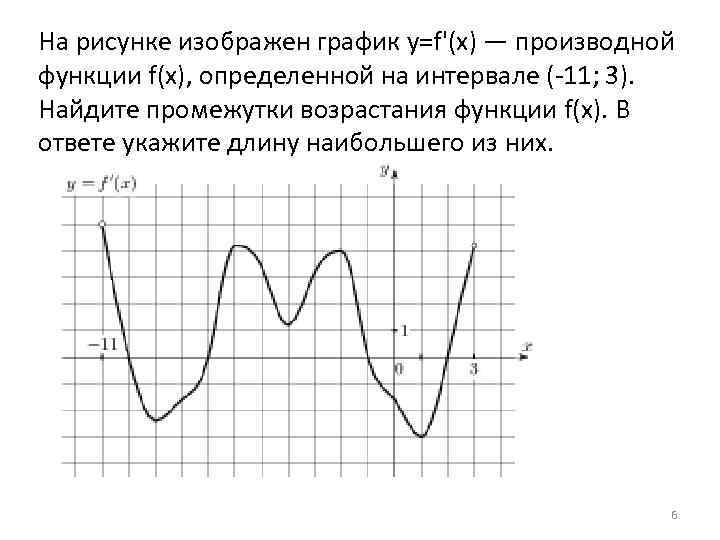
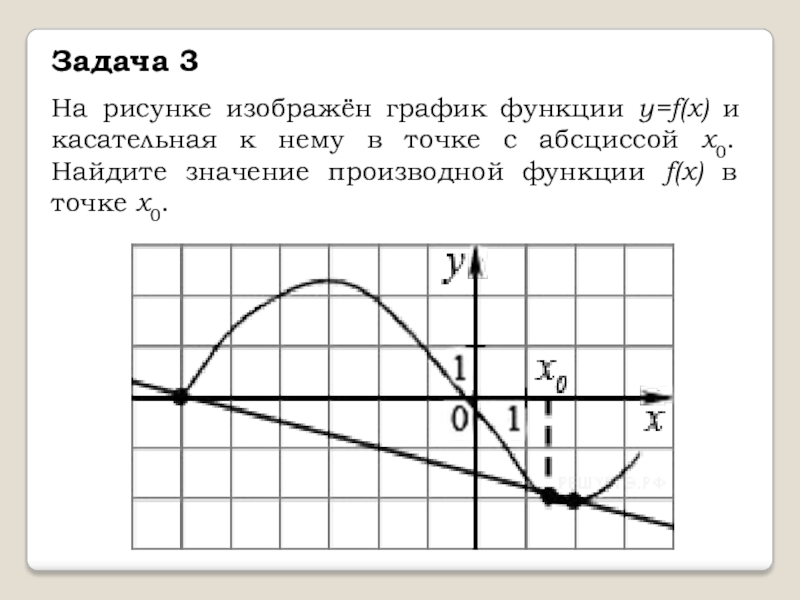
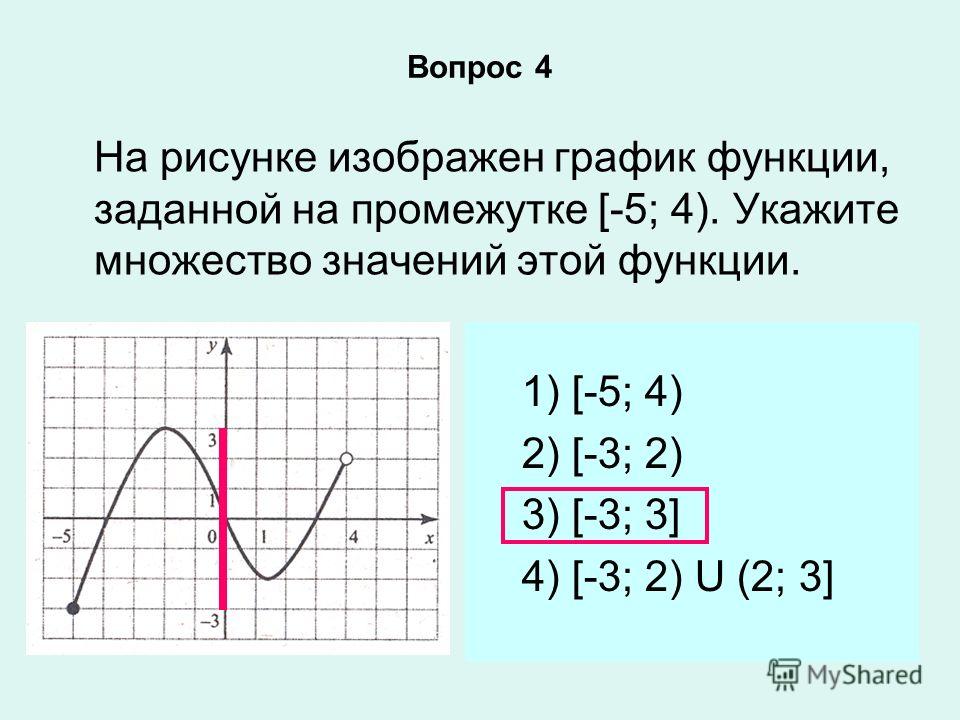
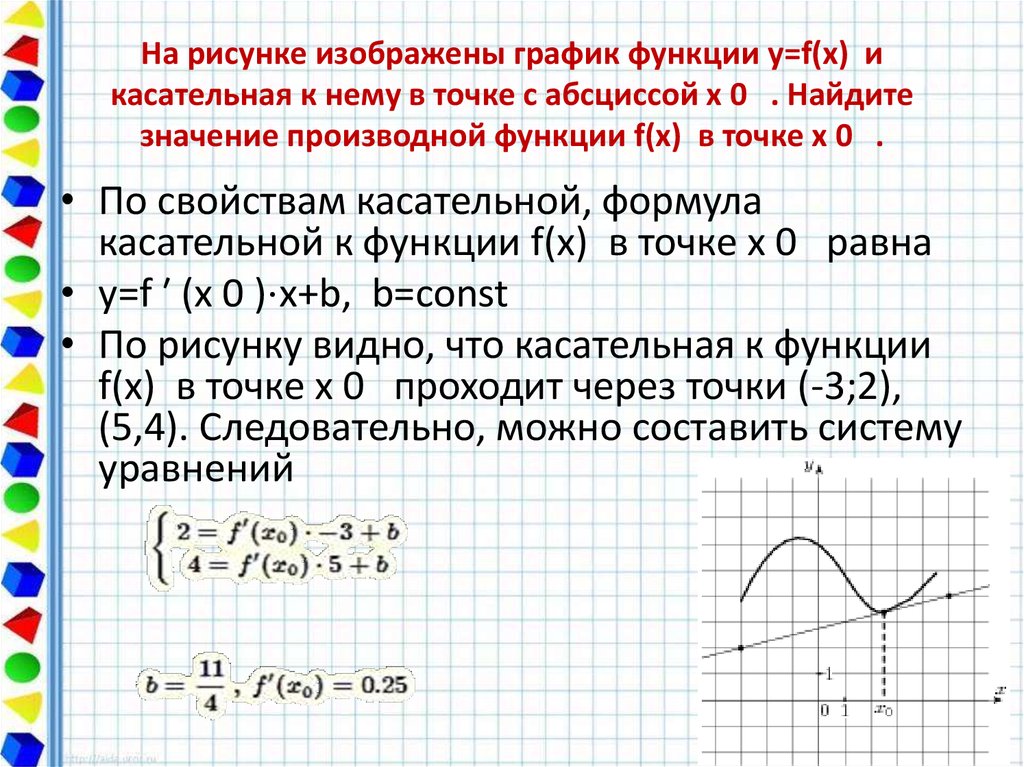
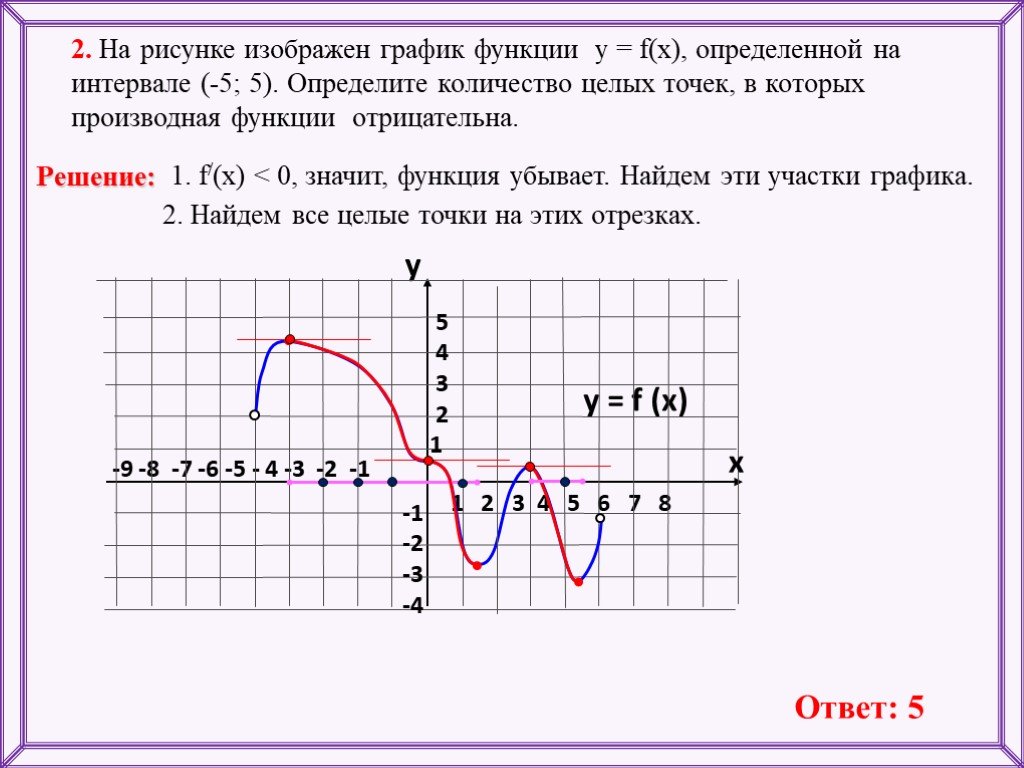
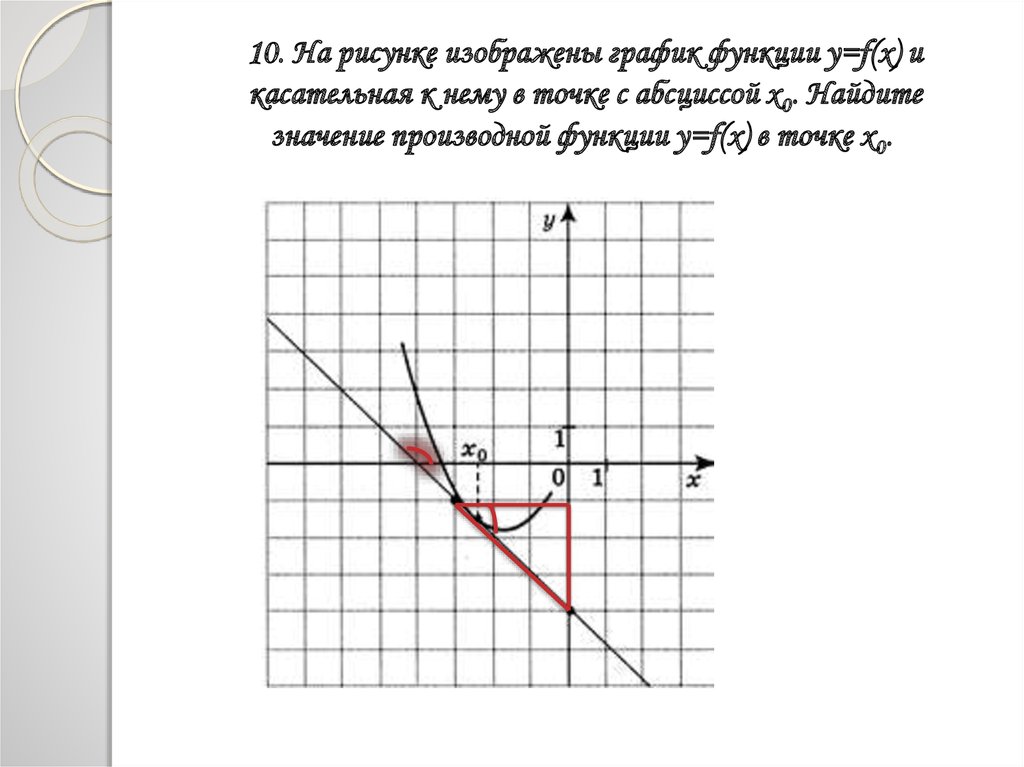
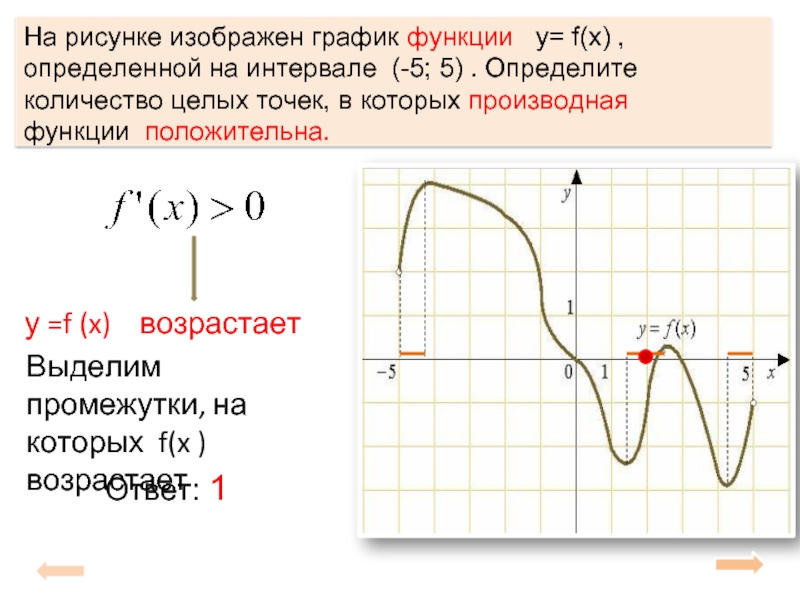
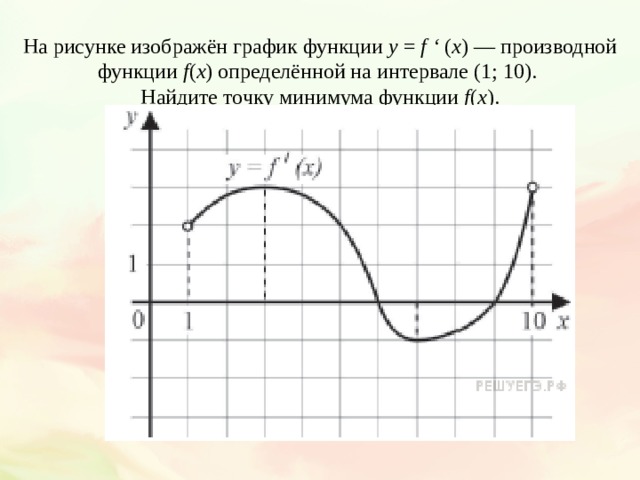
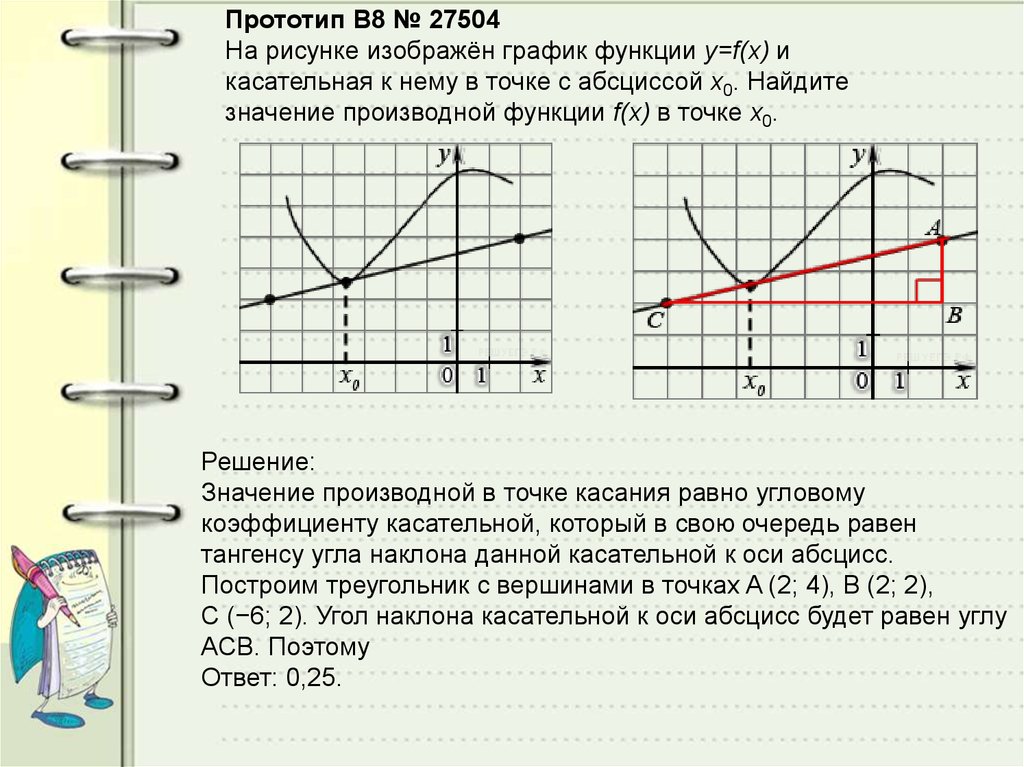
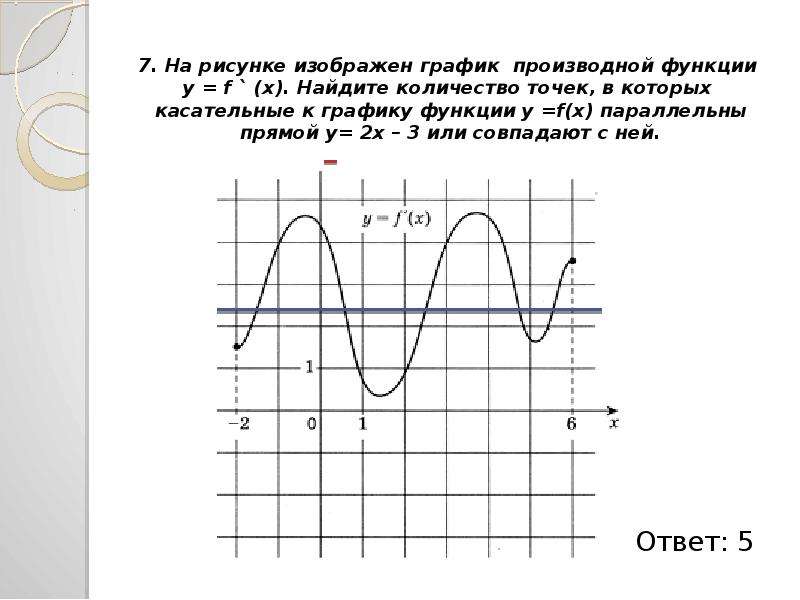
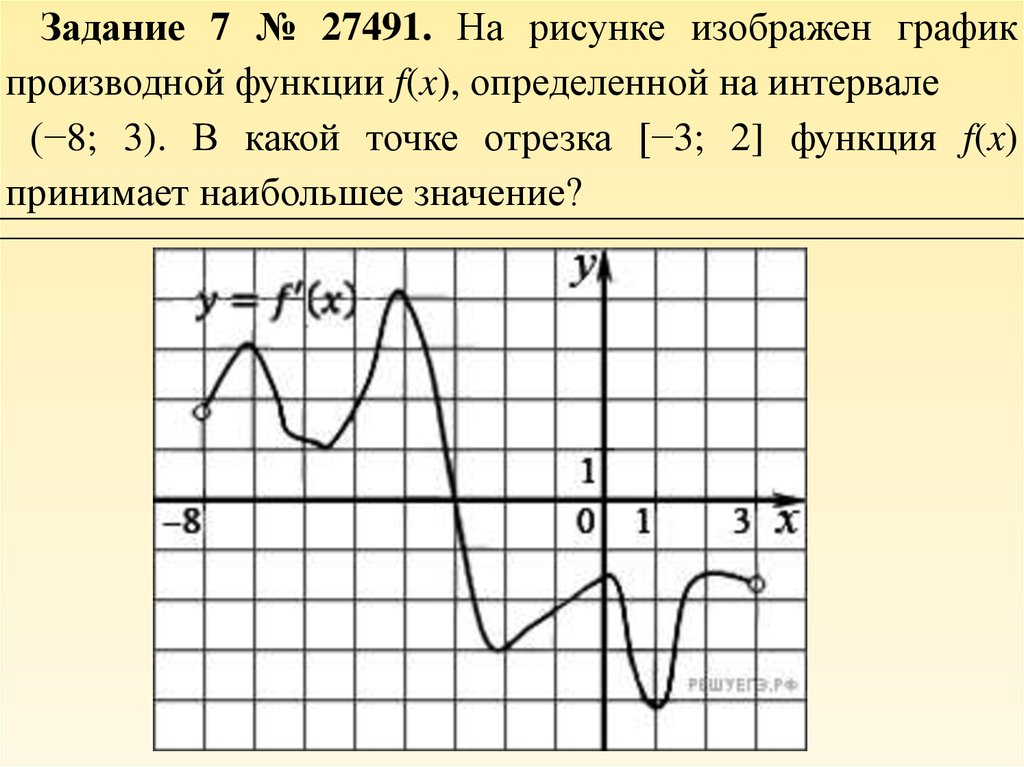
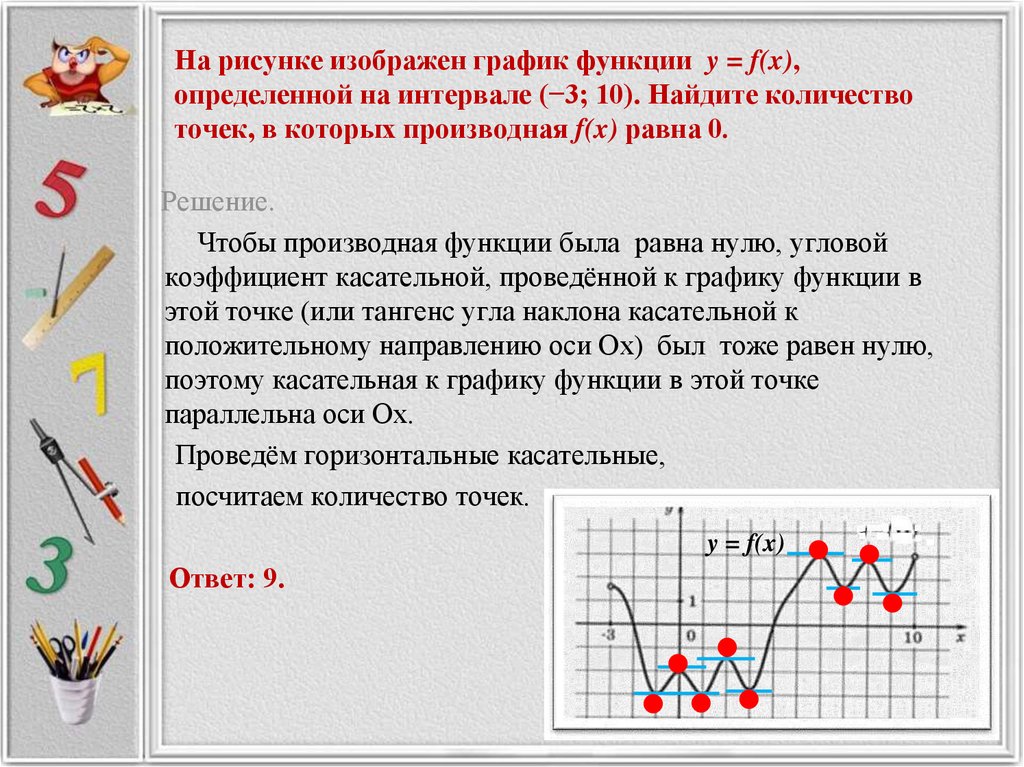
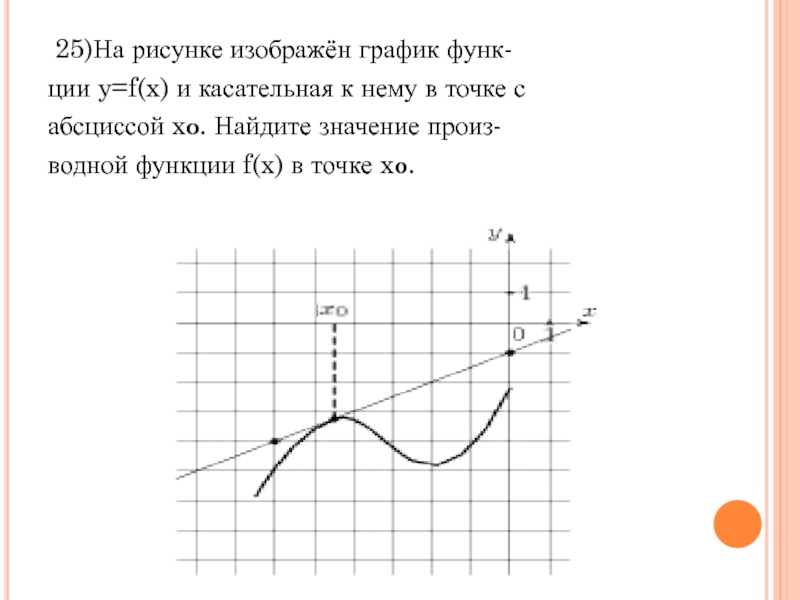
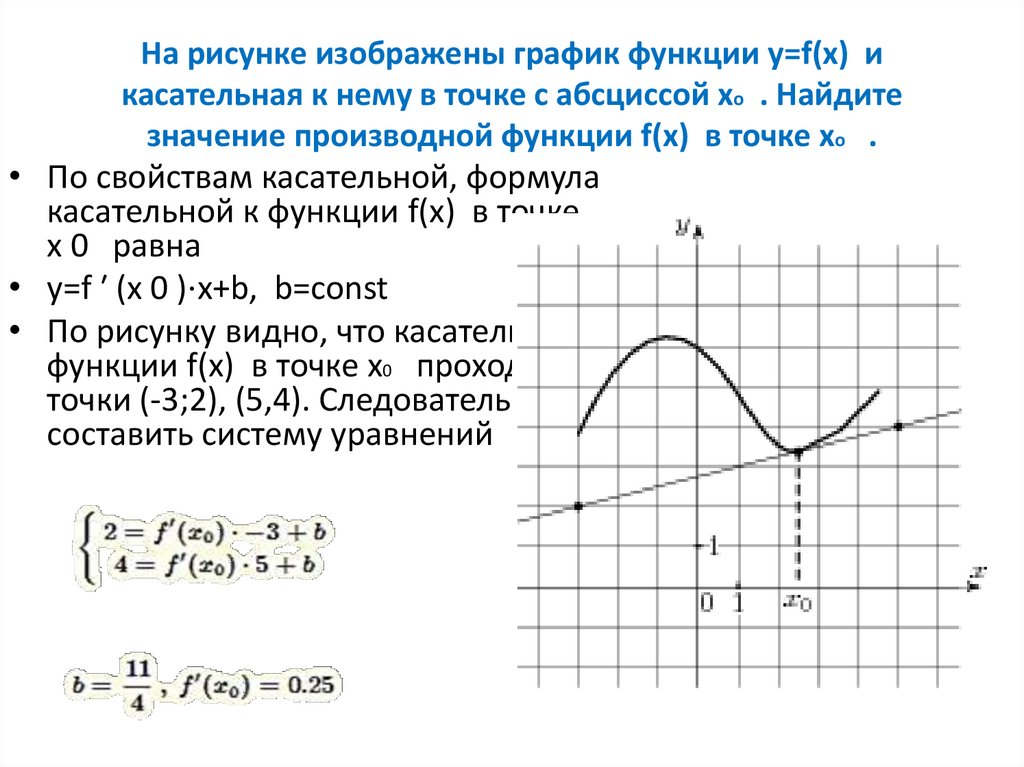
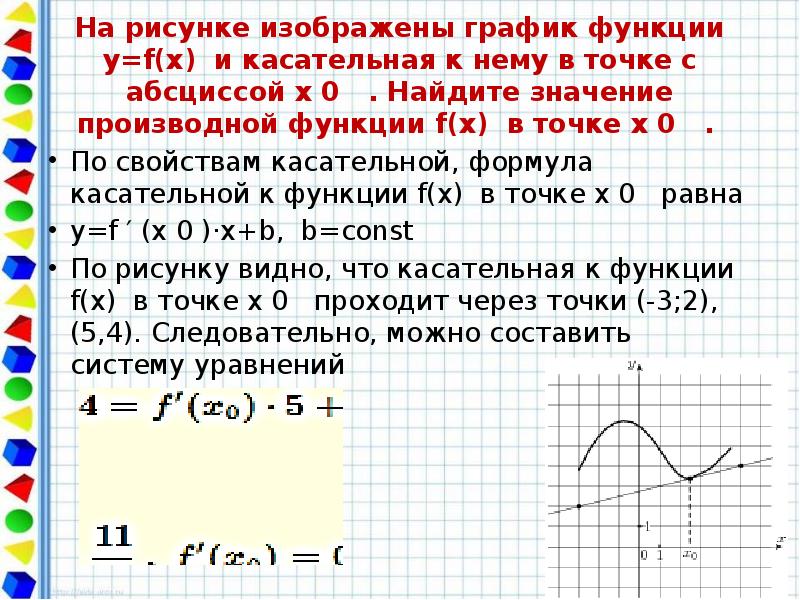
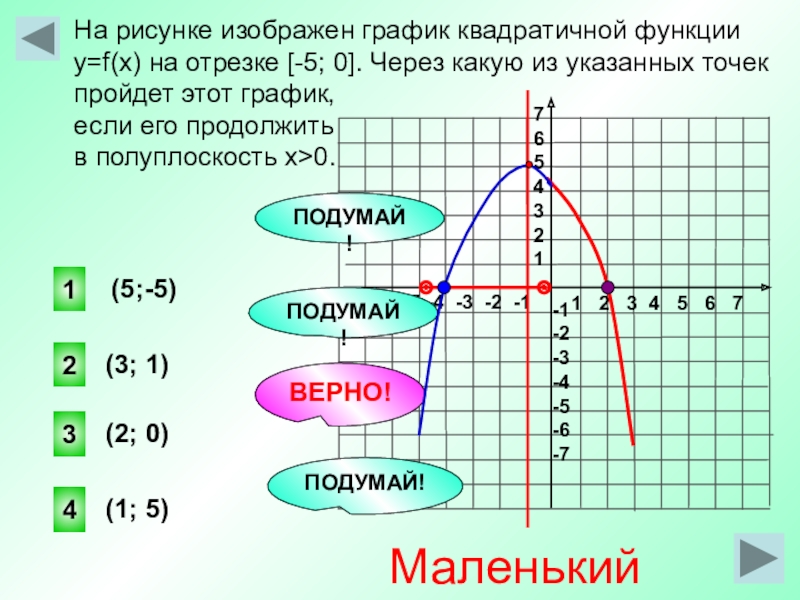
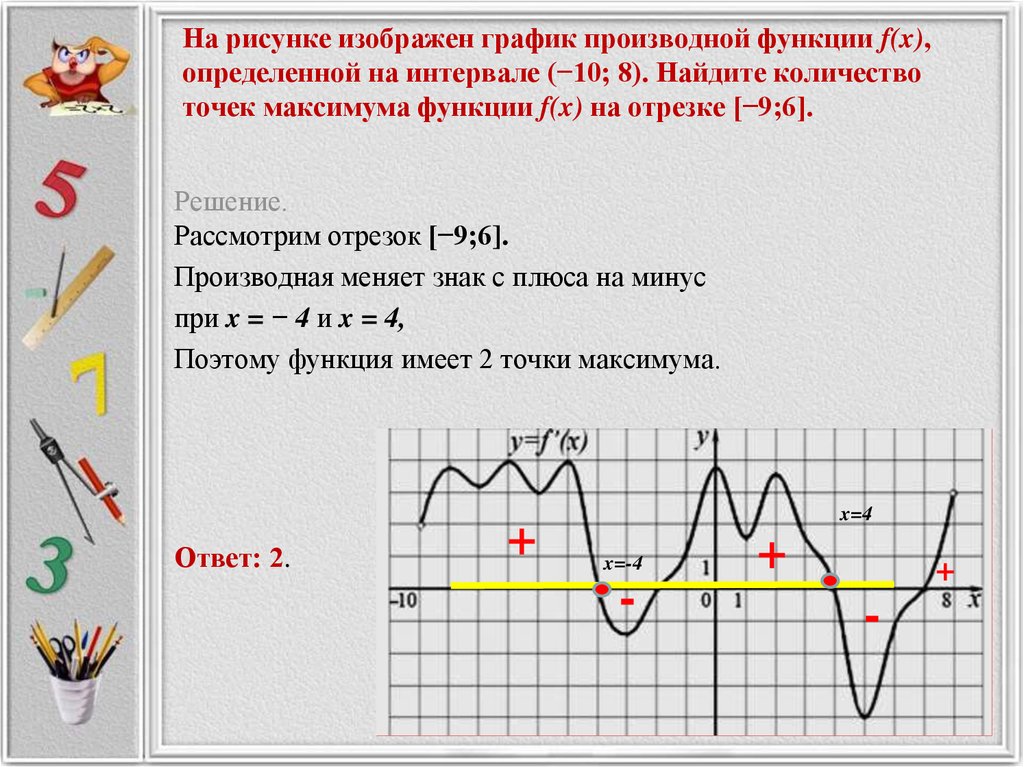
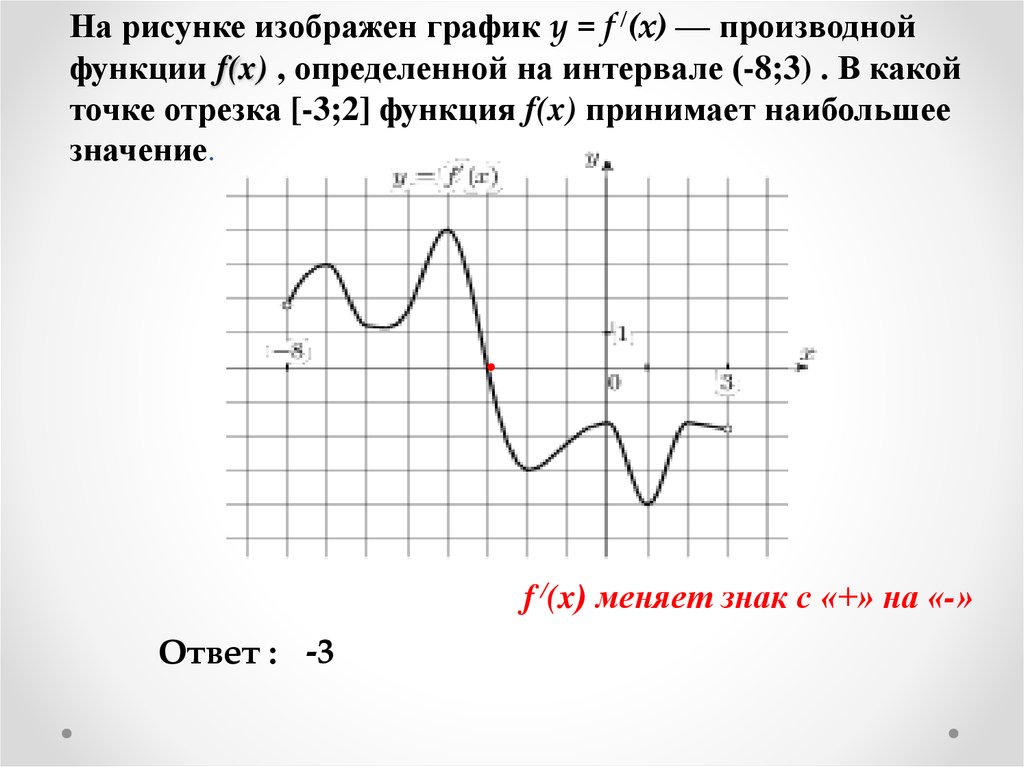
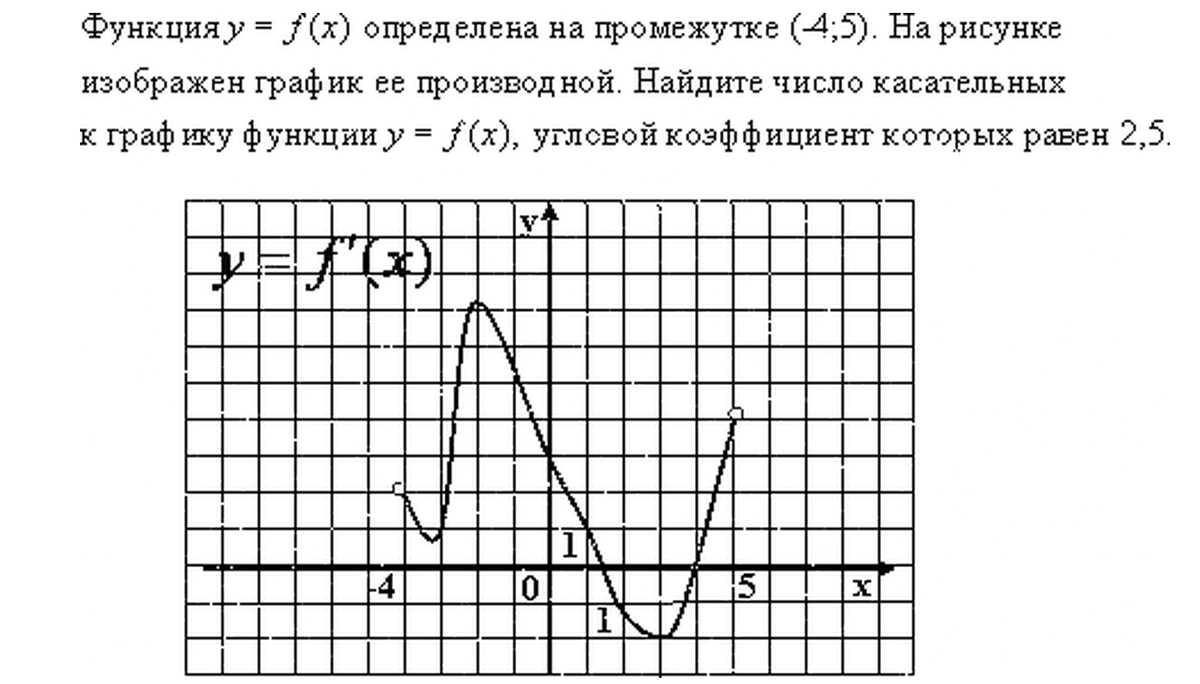
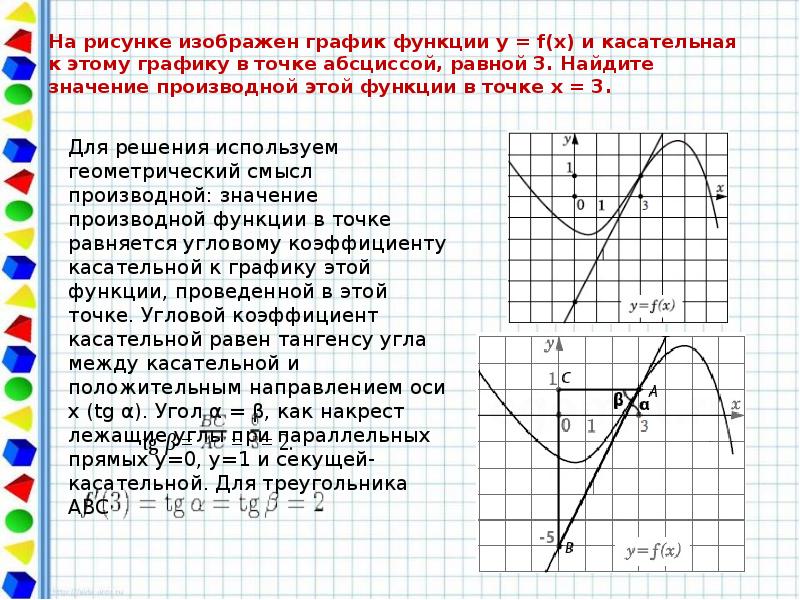
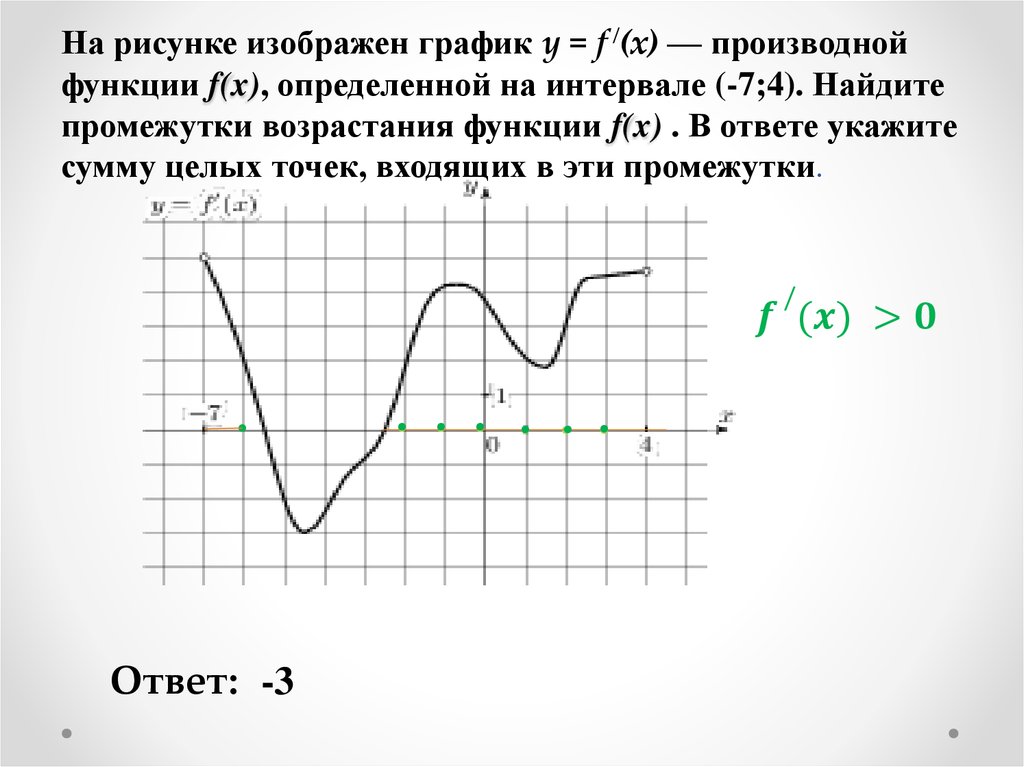
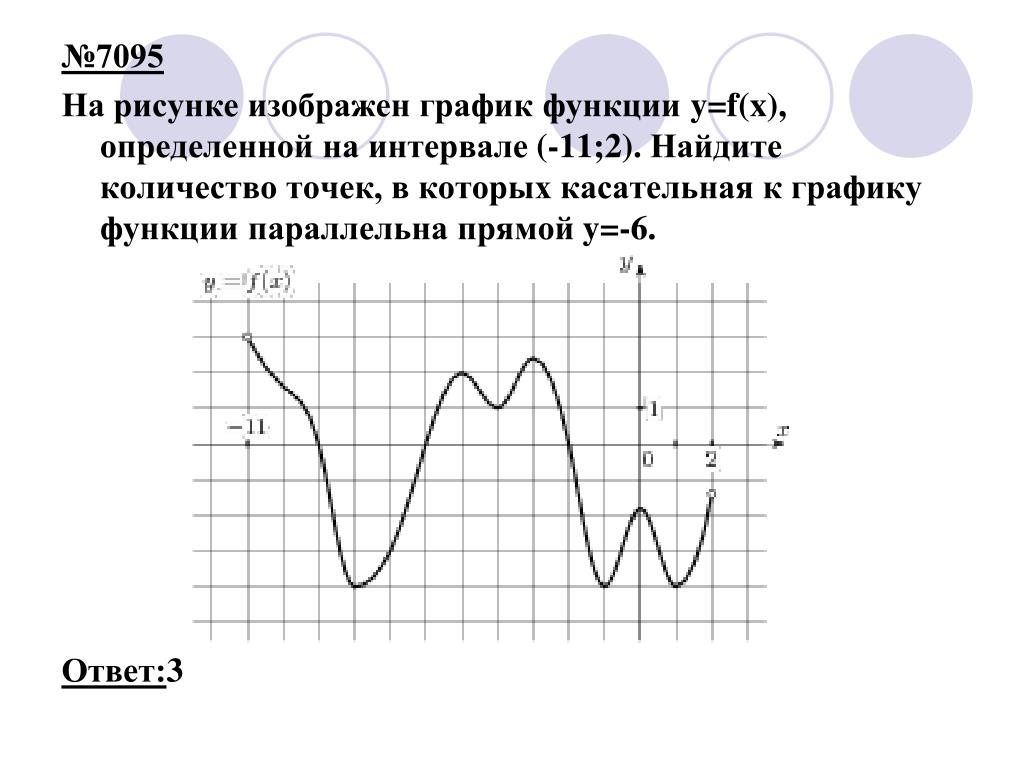
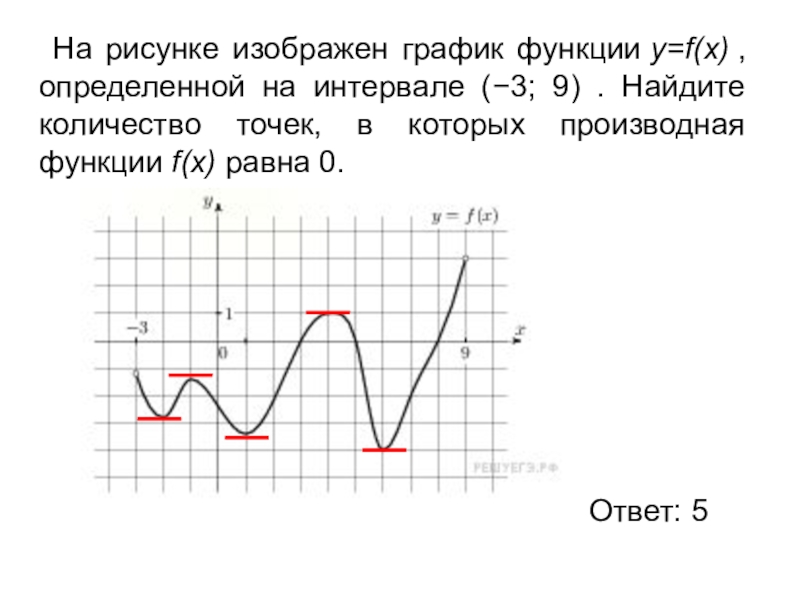
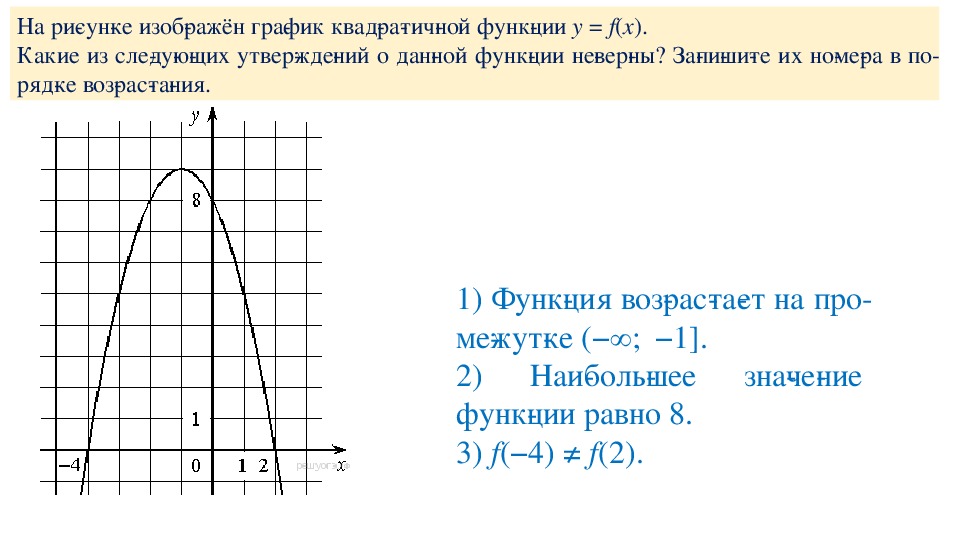
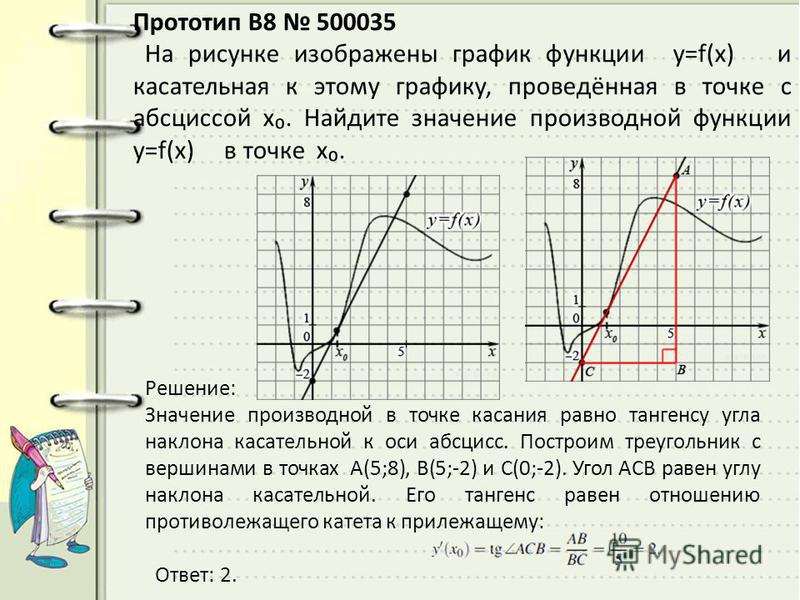
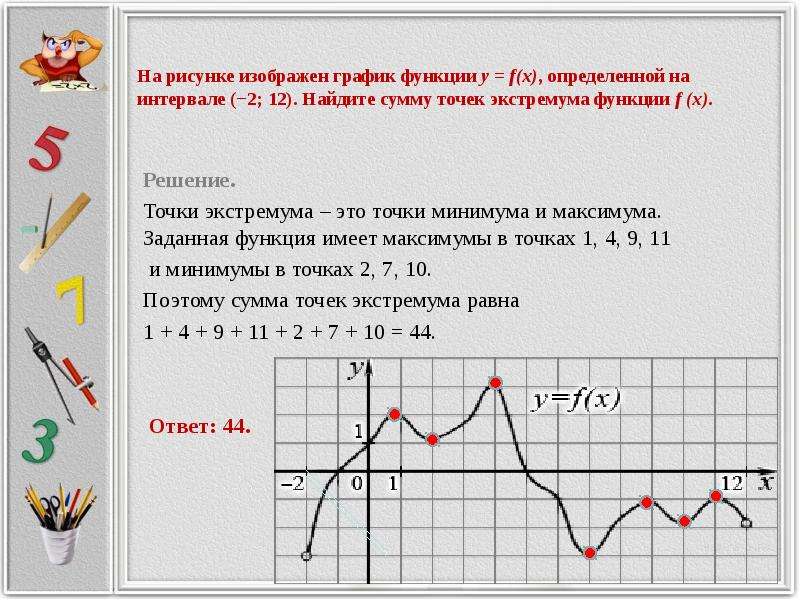
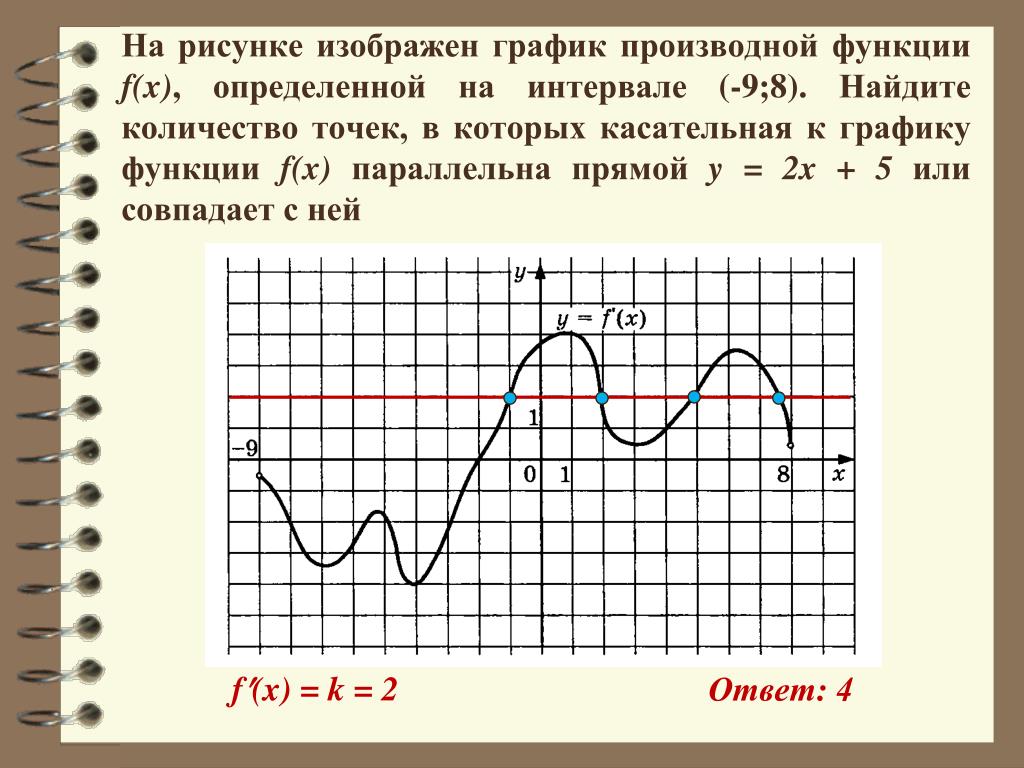
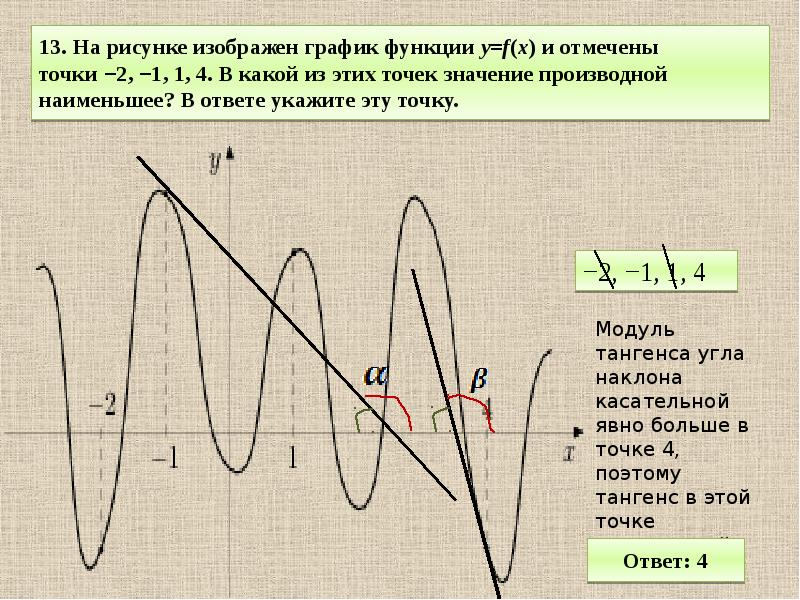
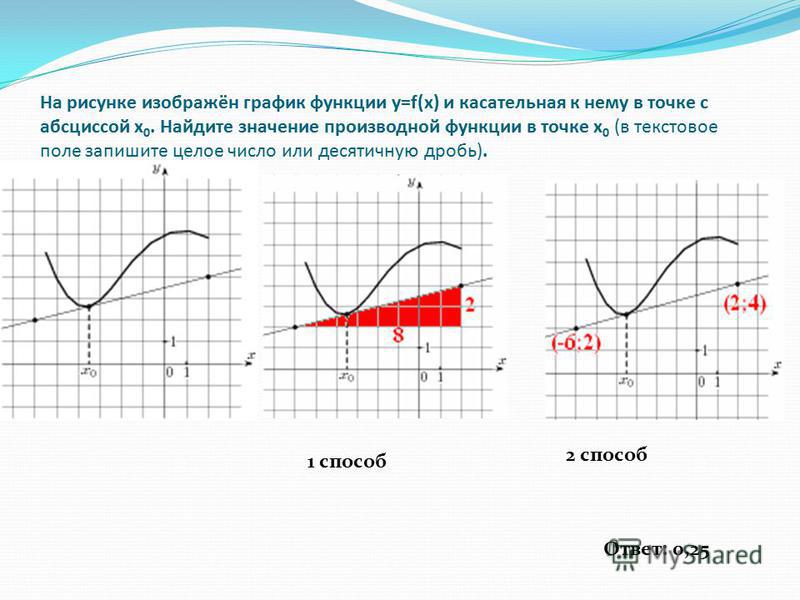
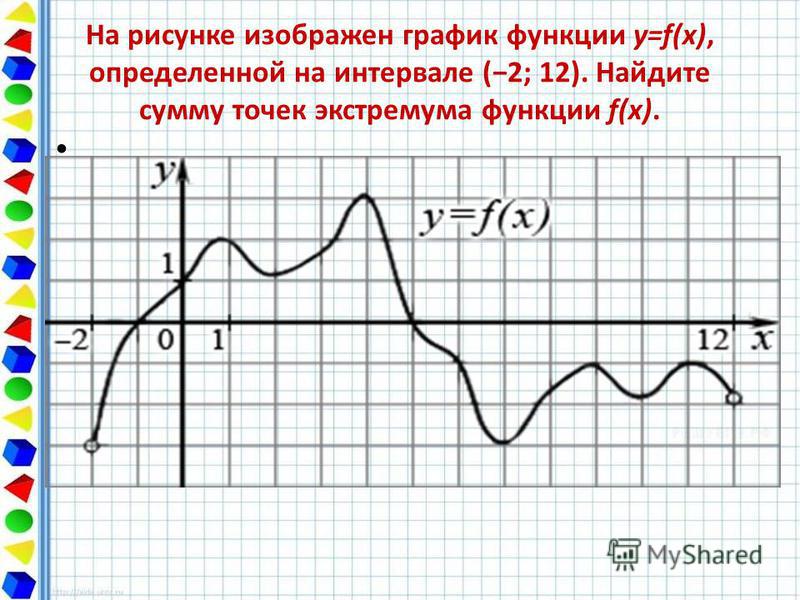
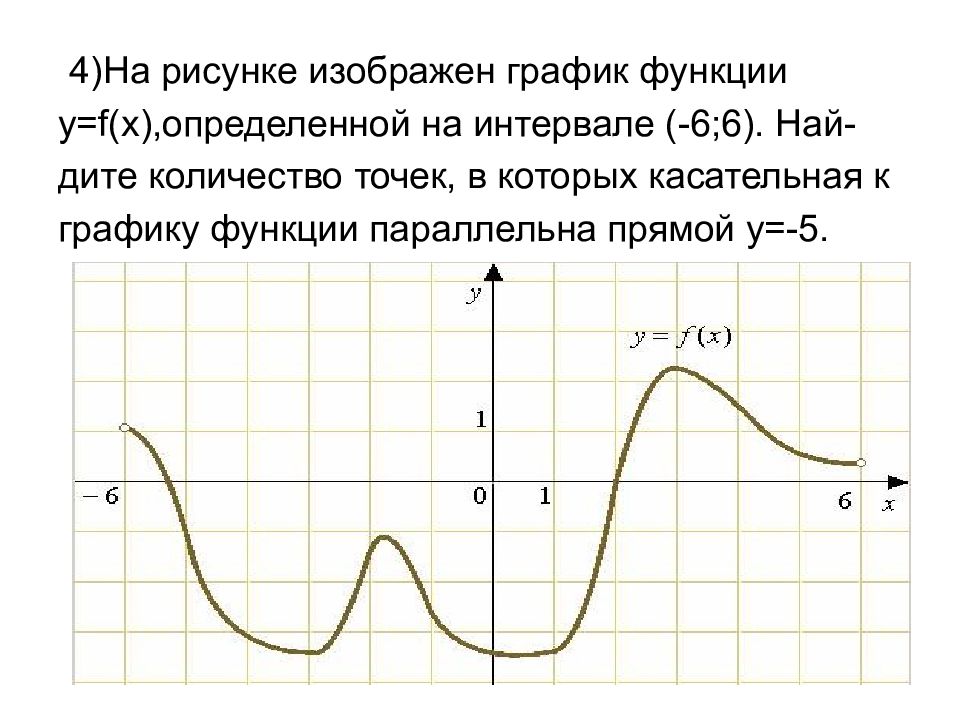
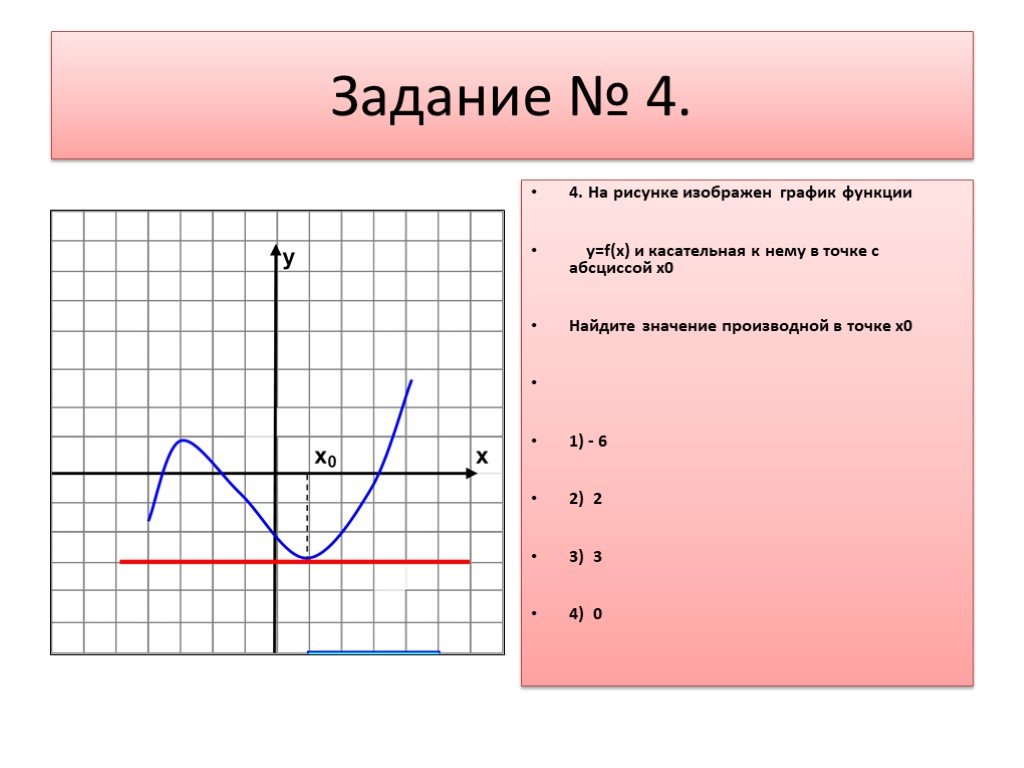
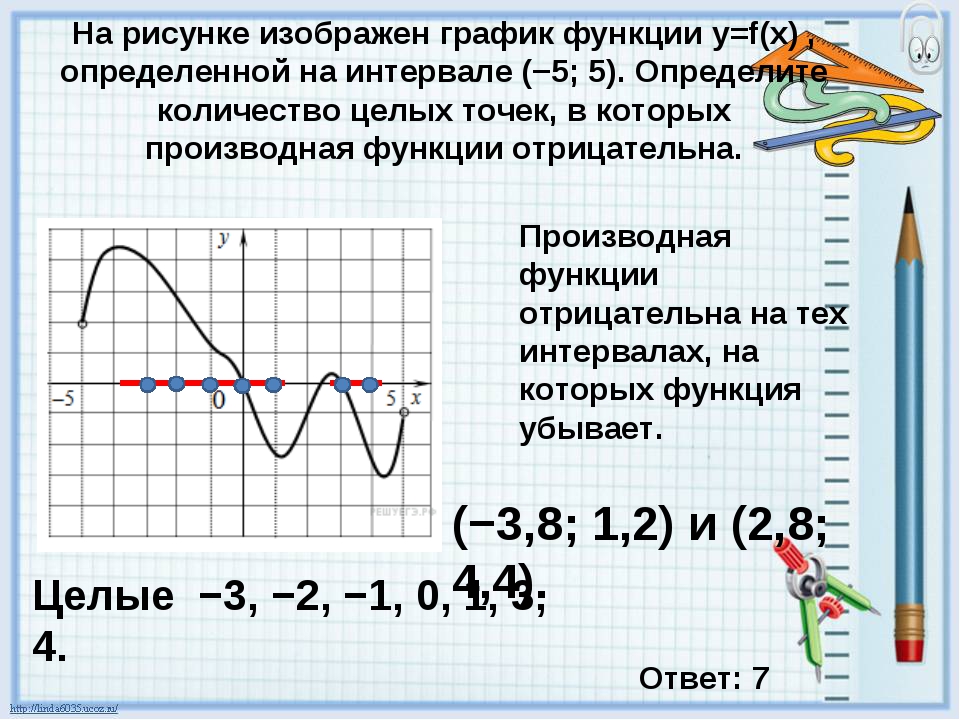
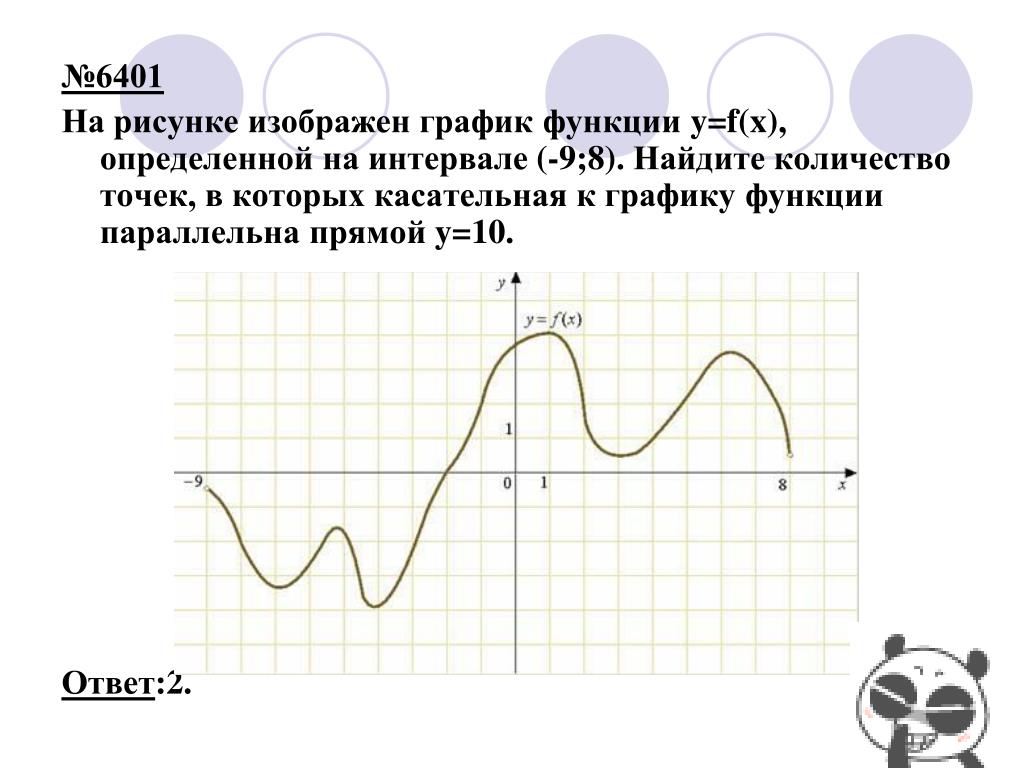
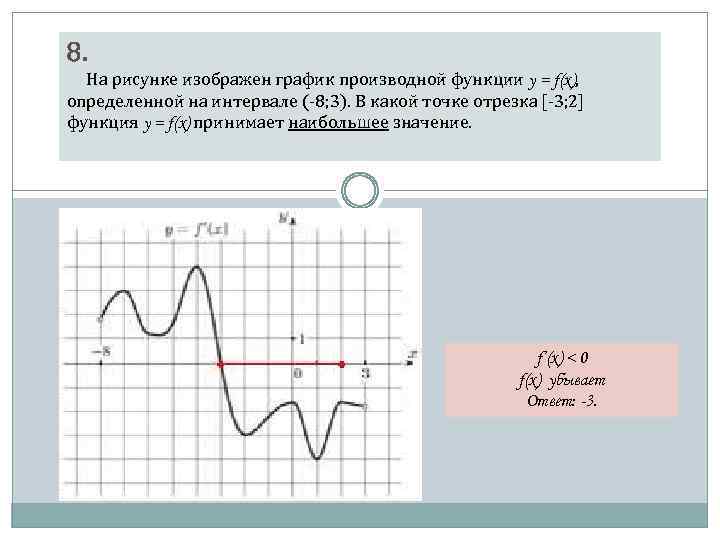
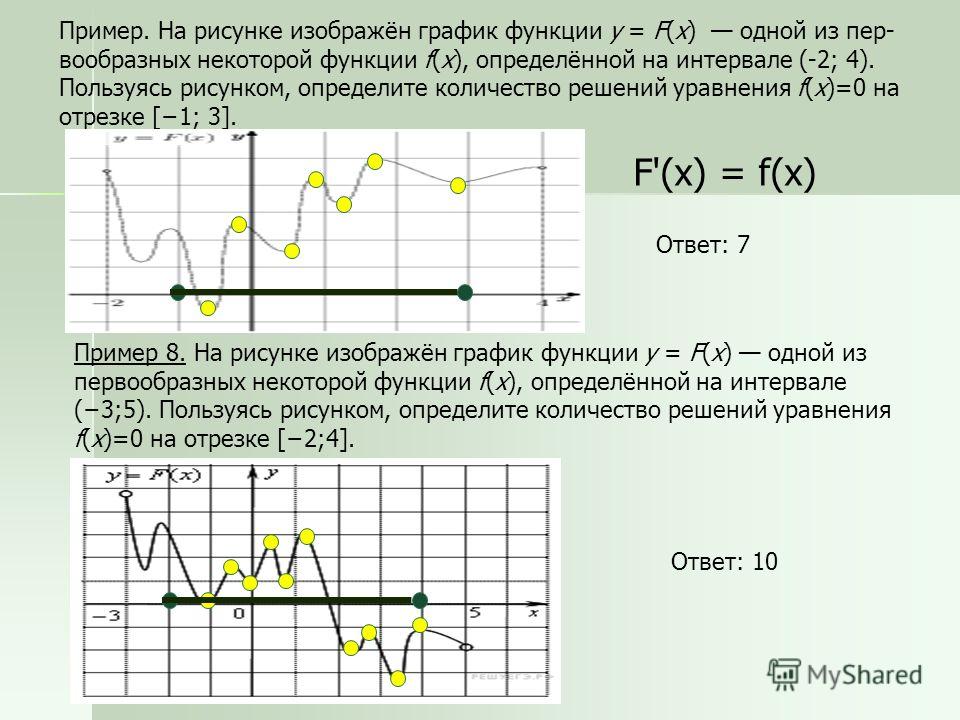
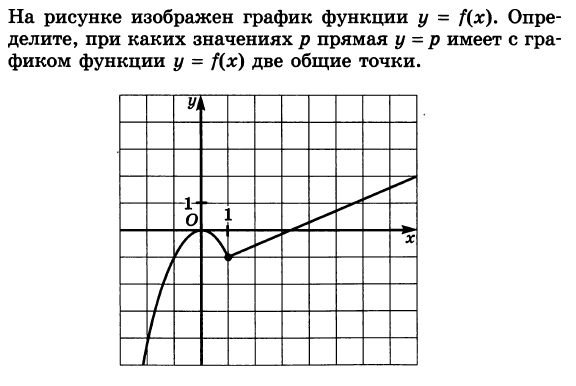
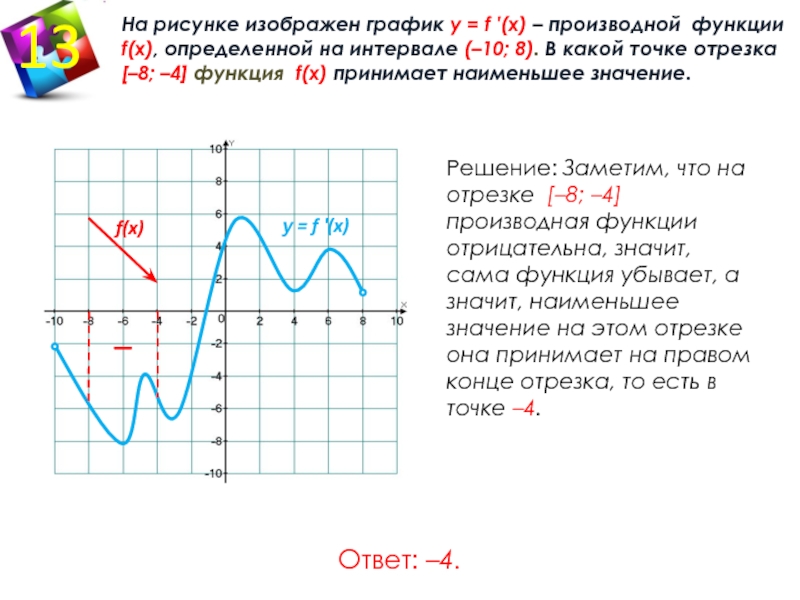
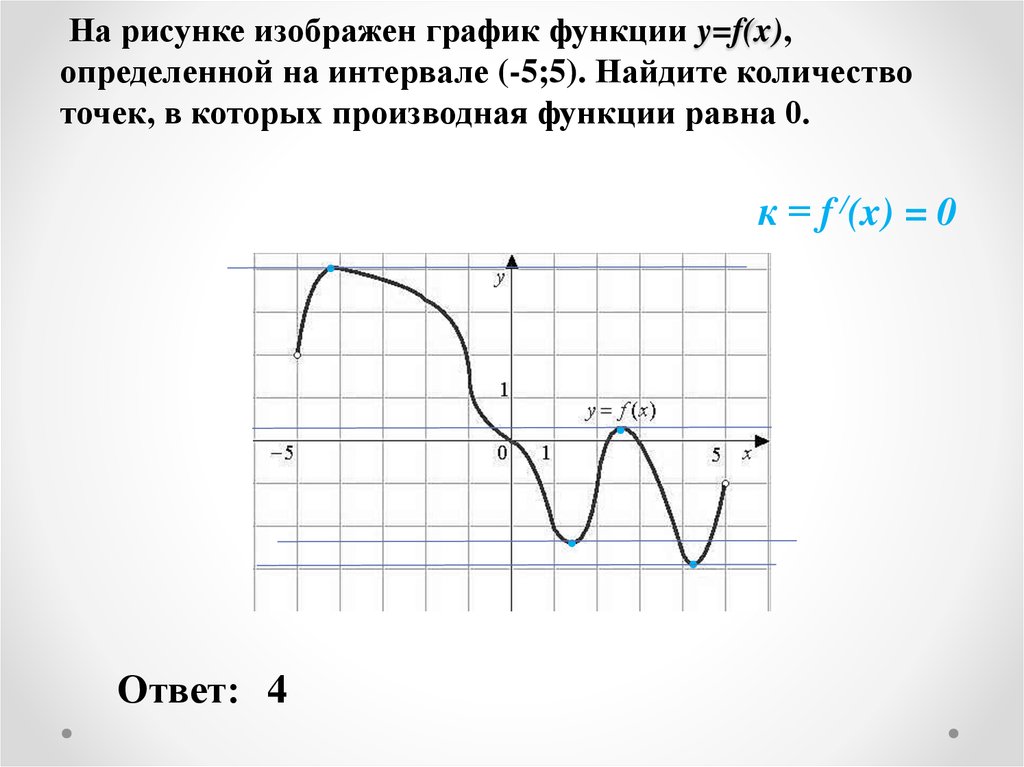
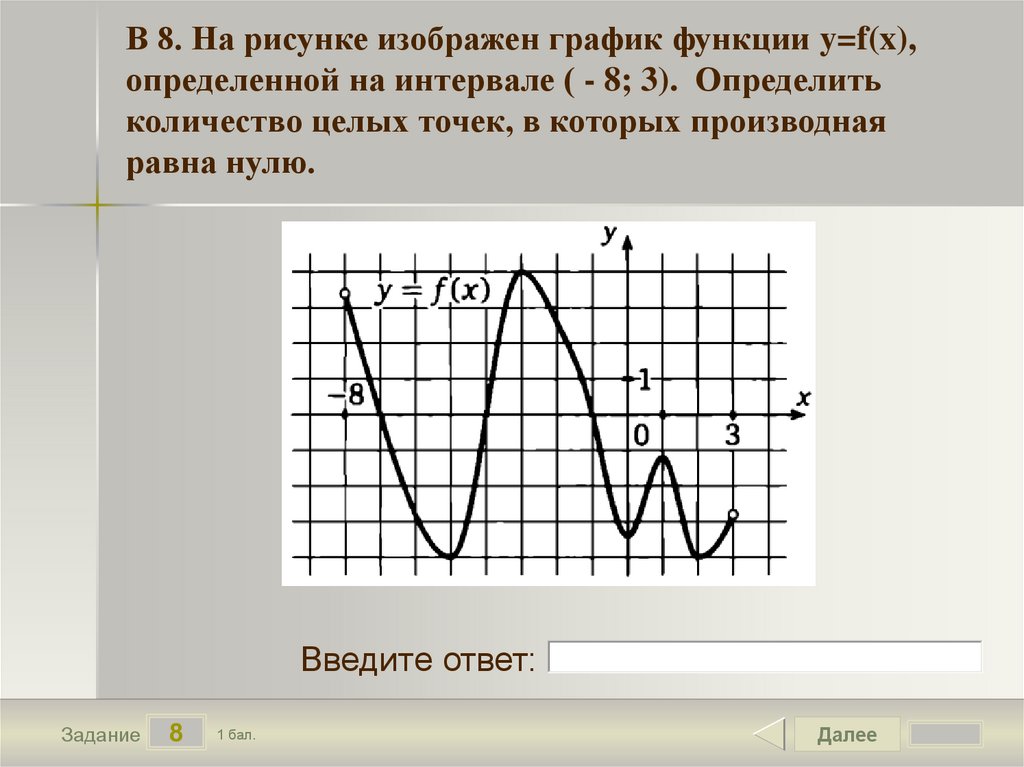
В начале статьи мы рассмотрим основные понятия, связанные с графическим представлением функции \( y = f(x) \). График функции является ключевым инструментом в математическом анализе, позволяющим визуализировать взаимосвязь между переменными \( x \) и \( y \). На рисунке функции \( y = f(x) \) каждая точка графика соответствует паре значений \((x, f(x))\), где \( x \) — аргумент функции, а \( f(x) \) — её значение. Такое представление помогает наглядно анализировать свойства функции, такие как монотонность, экстремумы и асимптоты.
На рисунке функции y f x
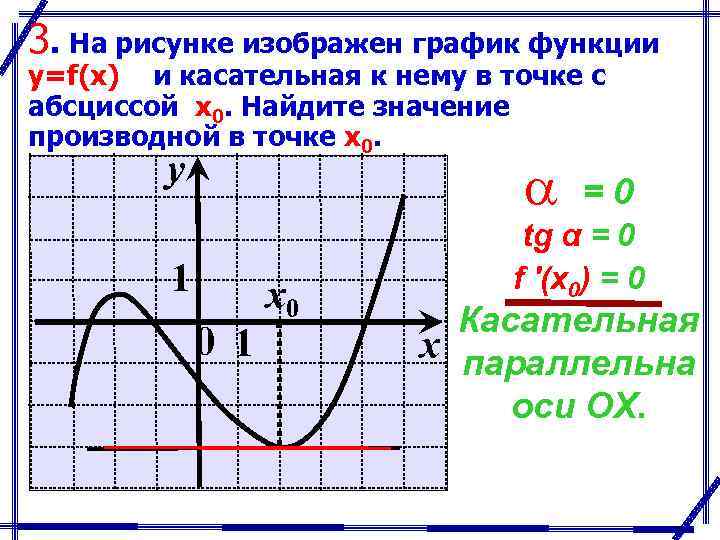
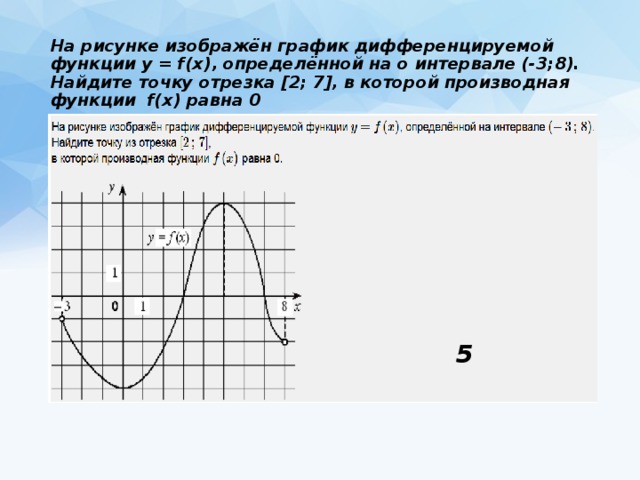
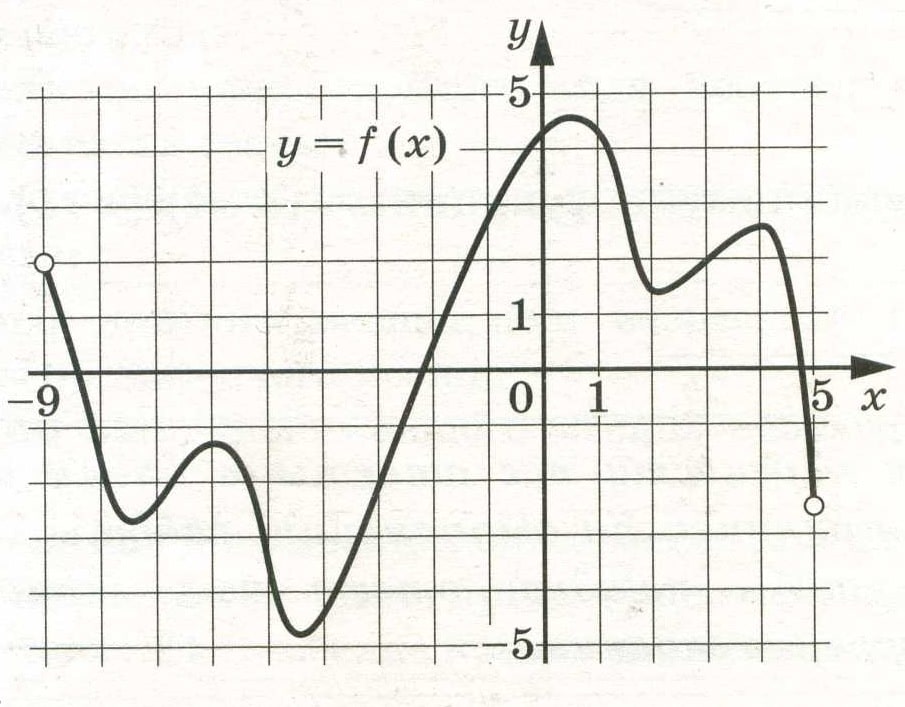
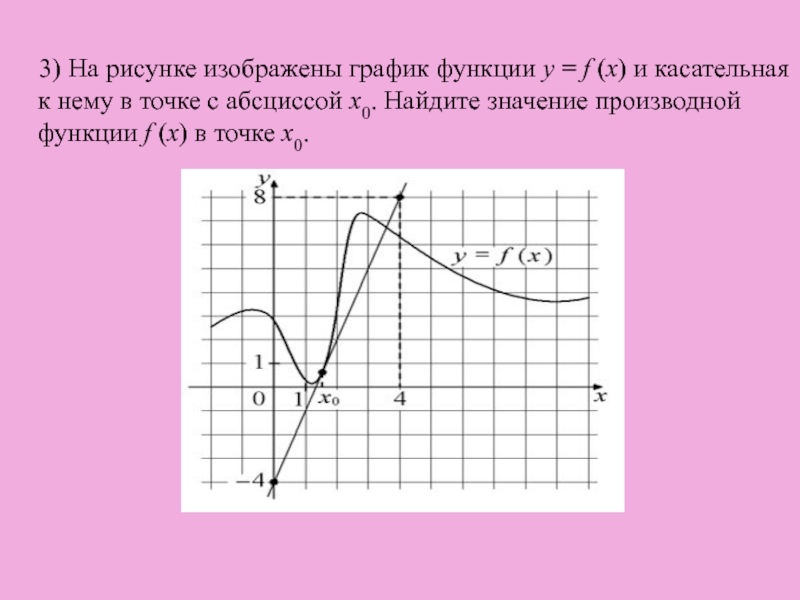
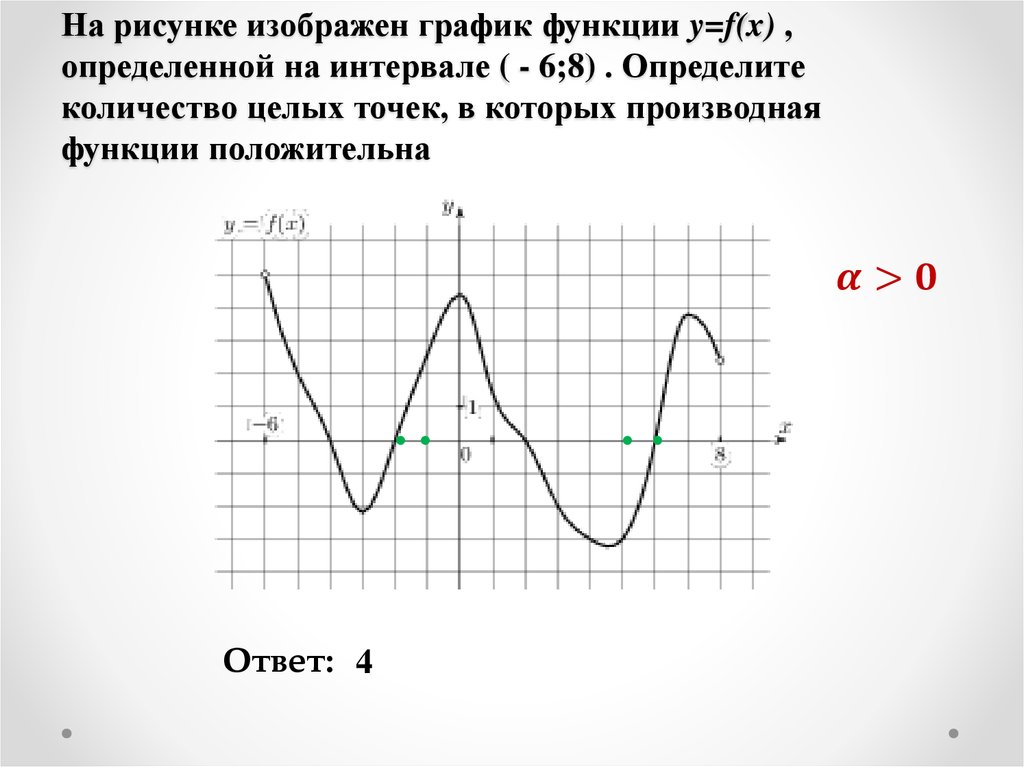

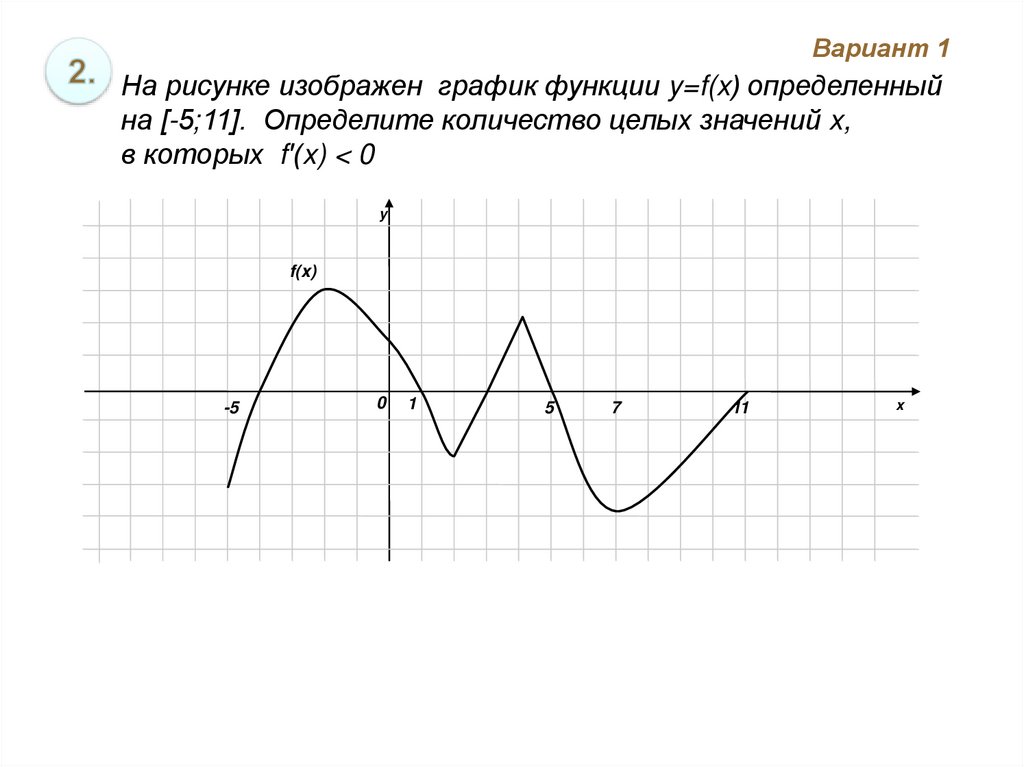
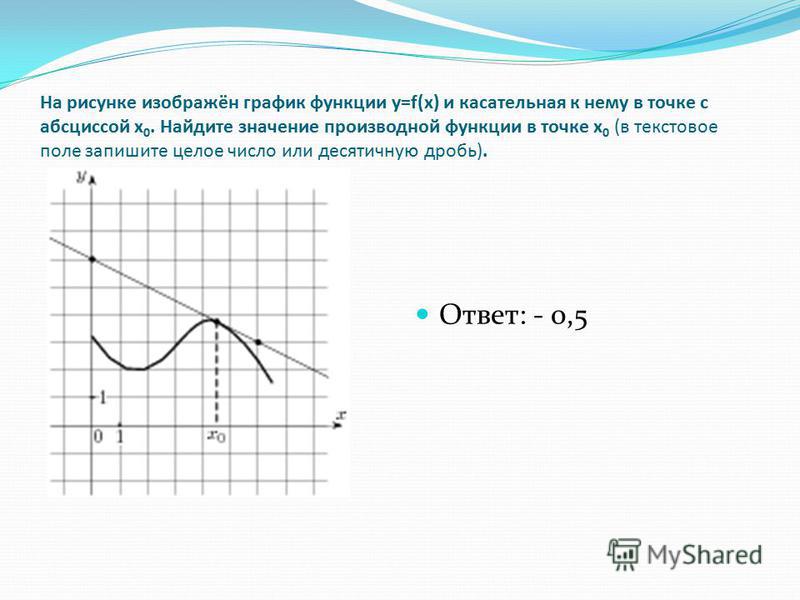
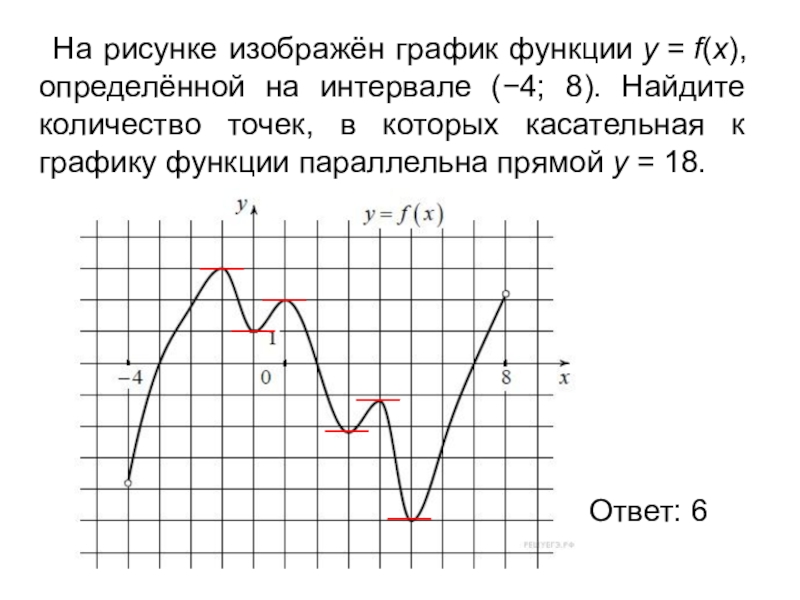

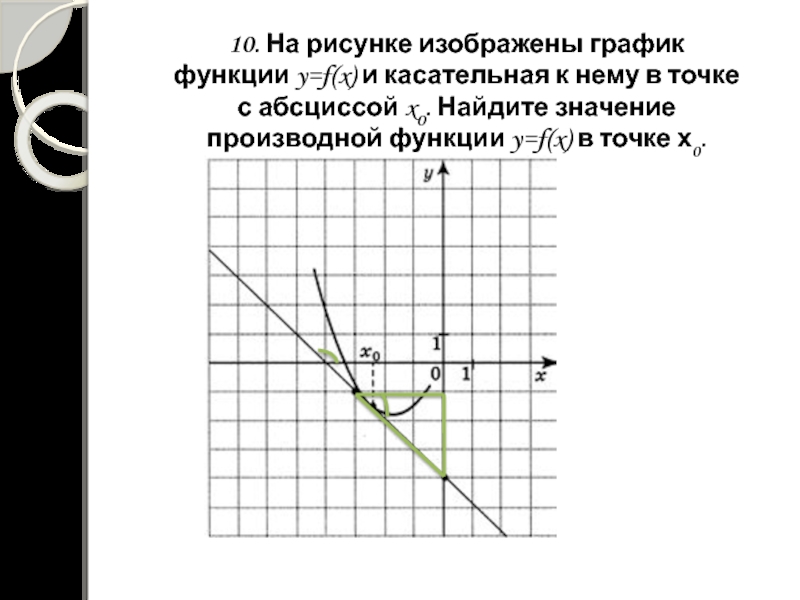
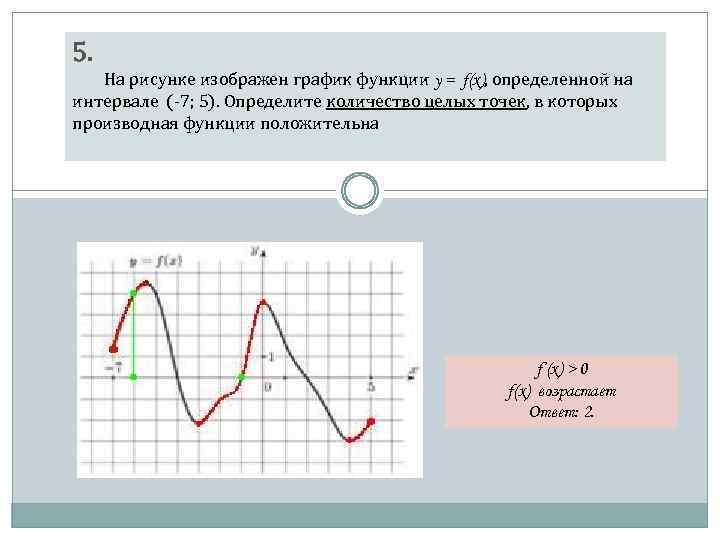
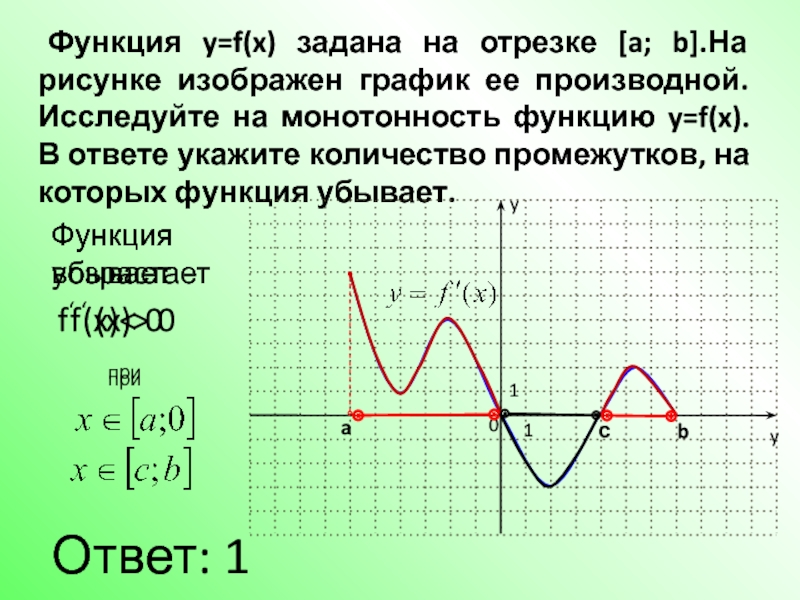
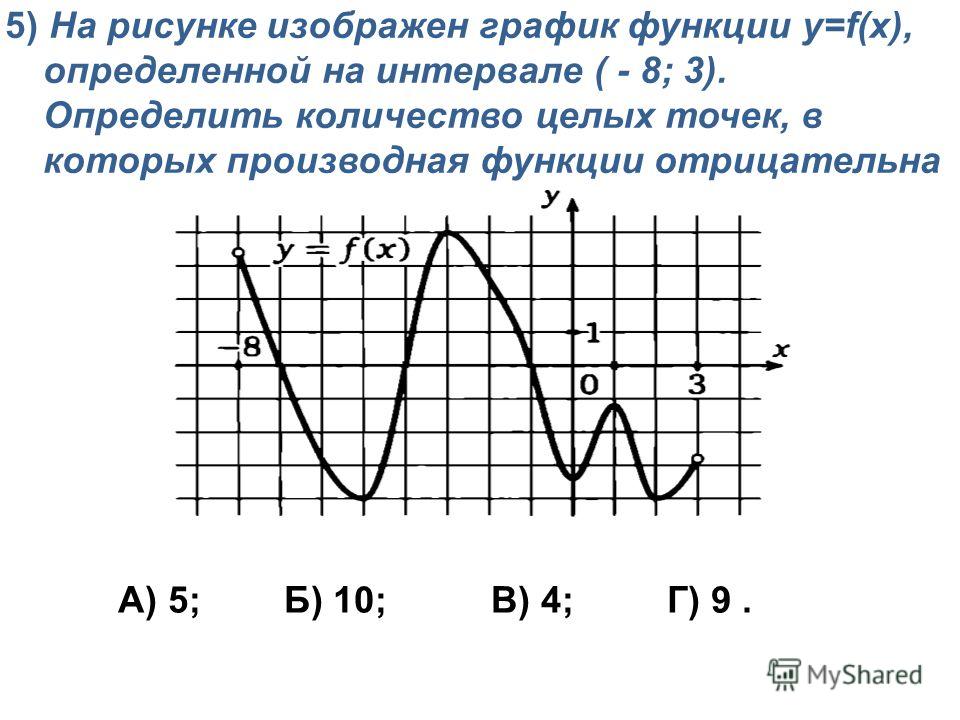
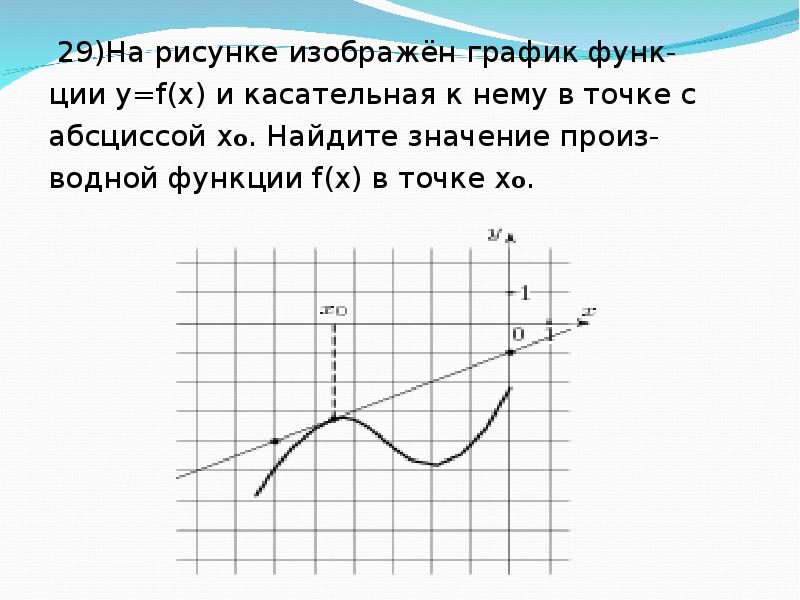
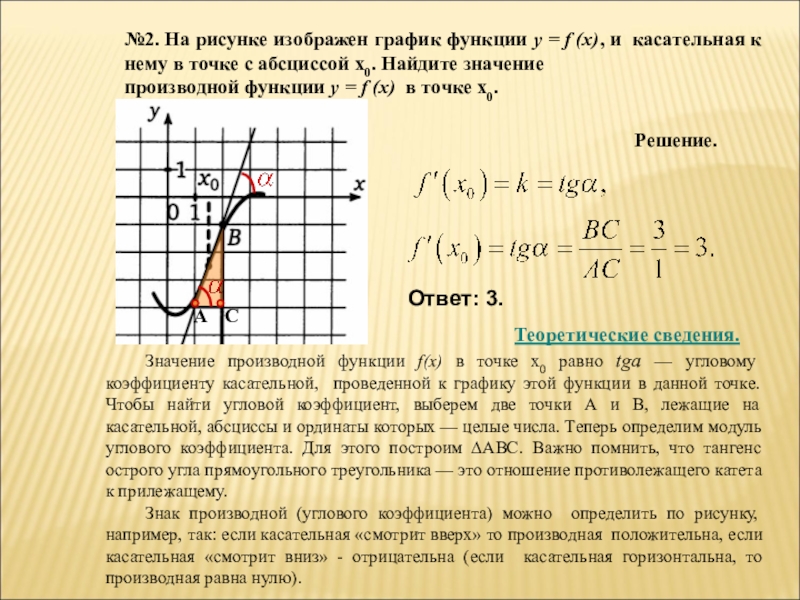
![На рисунке изображён график функции y=f(x) на отрезке [a;b].. График функции y = f(x) на отрезке [a;b]. Функция FX задана на отрезке a b рисунке. Непрерывная функция y f x задана на -10 11. На рисунке функции y f x. На рисунке изображён график функции y=f(x) на отрезке [a;b].. График функции y = f(x) на отрезке [a;b]. Функция FX задана на отрезке a b рисунке. Непрерывная функция y f x задана на -10 11.](https://fsd.multiurok.ru/html/2018/11/29/s_5bff09e03dc17/img12.jpg)